Tensiones o esfuerzos mecánicos (3)
2015-08-14
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En el primer artículo empezamos a ver el concepto de las fuerzas por unidad de superficie en el seno de un medio continuo: el vector tensión cuyas componentes vimos en el artículo de ayer. Hoy vamos a ver cómo representar las tensiones mediante una aplicación lineal.
Las tensiones como aplicación lineal
Analicemos lo que ocurre en un subdominio infinitesimal en el seno de un medio continuo. Este subdominio tiene forma de tetraedro como en la siguiente figura:
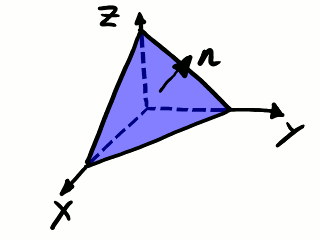
Subdominio tetraédrico. Tres caras son perpendiculares entre sí y
sirven para definir un sistema de coordenadas.
Este subdominio de volumen V y superficie de contorno S está sometido a fuerzas por unidad de superficie t (las tensiones) por su contorno y a fuerzas distribuidas f por su volumen. Bajo la acción de estas fuerzas, el material, que tiene una densidad ρ, experimenta una aceleración a de acuerdo con la ley de la cantidad de movimiento:
∫∫∫V ρ a dV = ∫∫∫V f dV + ∫∫S t dS.
Ahora escalemos el tetraedro hasta hacerlo muy, muy pequeño. El volumen va con el cubo del factor de escala, mientras que la superficie del contorno va con el cuadrado del factor de escala. Por lo tanto, las integrales de volumen van con la tercera potencia de una cantidad muy pequeña, mientras que la integral de superficie va solamente con la segunda potencia. Las integrales de volumen se convierten en infinitésimos despreciables frente a la integral de superficie y, en el límite, nos quedamos solamente con esta última integral, la de las tensiones.
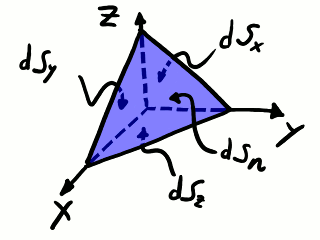
Subdominio tetraédrico infinitesimal.
Describamos un poco la geometría de nuestro tetraedro infinitesimal, que tiene tres caras perpendiculares entre sí de manera que definen un triedro que nos sirve para establecer un sistema de coordenadas cartesianas. Las normales exteriores a estas caras apuntan en las direcciones de los ejes coordenados en sentido negativo. La cara perpendicular al eje X tiene superficie dSx. La cara perpendicular al eje Y tiene superficie dSy. La cara perpendicular al eje Z tiene superficie dSz. La cuarta cara, cuya normal es n, tiene superficie eje X tiene superficie dSn. Las componentes del vector normal n a esta cara son nx según el eje X, ny según el eje Y y nz según el eje Z. Las superficies de las tres primeras caras están relacionadas con la superficie de la cuarta cara a través de las componentes de la normal que acabamos de definir:
dSx = dSn nx;
dSy = dSn ny;
dSz = dSn nz.
Listas las definiciones geométricas, ahora hace falta establecer la notación para las tensiones. La tensión medida en la cara perpendicular al eje X tiene componentes σxx (según el eje X negativo), σxy (según el eje Y negativo) y σxz (según el eje Z negativo). La tensión medida en la cara perpendicular al eje Y tiene componentes σyx (según el eje X en sentido negativo), σyy (según el eje Y en sentido negativo) y σyz (según el eje Z en sentido negativo). La tensión medida en la cara perpendicular al eje Z tiene componentes σzx (según el eje X en sentido negativo), σzy (según el eje Y en sentido negativo) y σzz (según el eje Z en sentido negativo). Finalmente, la tensión medida en la cuarta cara tiene componentes tx (según el eje X en sentido positivo), ty (según el eje Y en sentido positivo) y tz (según el eje Z en sentido positivo). Este criterio de signos, con las componentes en sentido negativo en las tres primeras caras y en sentido positivo en la cuarta cara, es para que nos queden las cuentas un poco más ordenadas al plantear la ecuación de la cantidad de movimiento.
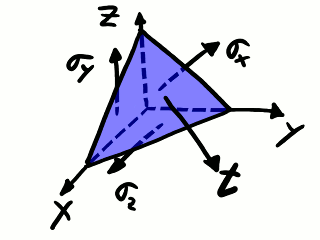
Tetraedro infinitesimal bajo tensiones.
Ahora que está todo definido, podemos plantear la ecuación de la cantidad de movimiento. Vimos que los términos volumétricos eran despreciables y solamente quedaban las integrales de superficie de las tensiones. Para un volumen infinitesimal, salen tres ecuaciones, una por cada componente:
0 = −σxx dSx − σyx dSy − σzx dSz + tx dSn;
0 = −σxy dSx − σyy dSy − σzy dSz + ty dSn;
0 = −σxz dSx − σyz dSy − σzz dSz + tz dSn.
Ahora bien, las superficies dSx, dSy y dSz están relacionadas con dSn como vimos antes. Podemos introducir las relaciones en las ecuaciones de la cantidad de movimiento y dejarlas así:
0 = −σxx dSn nx − σyx dSn ny − σzx dSn nz + tx dSn;
0 = −σxy dSn nx − σyy dSn ny − σzy dSn nz + ty dSn;
0 = −σxz dSn nx − σyz dSn ny − σzz dSn nz + tz dSn.
Esto es lo mismo que decir lo siguiente:
tx = σxx nx + σyx ny + σzx nz;
ty = σxy nx + σyy ny + σzy nz;
tz = σxz nx + σyz ny + σzz nz.
La dirección n es cualquiera que escojamos, así que tenemos una ley general que explica cómo varía el vector de tensión en función de la dirección en la que se mide. Esta ley es una aplicación lineal sobre el vector unitario que marca la dirección. Podemos dejar escrita esta relación de forma matricial:
tT = nT ⋅ σ.
En esta relación, tT es el vector tensión representado como una matriz fila:
| tx | ty | tz |
| nx | ny | nz |
| σxx | σxy | σxz |
| σyx | σyy | σyz |
| σzx | σzy | σzz |
Esto es tan importante que hay que repetirlo. En un punto dado, el vector tensión se calcula mediante una aplicación lineal sobre el vector unitario que marca la dirección de medida; esta aplicación lineal está representada mediante las componentes de una matriz cuadrada. Más adelante, veremos que lo propio es hablar de un tensor cuadradade tensiones.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/14/tensiones-o-esfuerzos-mecanicos-3/
