Septiembre de 2015
Calendario de artículos de de 2015
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | ||||
El trabajo y el calor en termodinámica
2015-09-30
En termodinámica, un sistema cerrado interactúa con su entorno mediante trabajo y mediante calor. Ambas magnitudes son energía en tránsito: el paso de energía de un sistema a otro y no la energía de un sistema en sí misma.
El trabajo se produce al aplicar una fuerza generalizada que provoca un desplazamiento generalizado: una fuerza aplicada sobre un pistón realiza trabajo cuando el pistón se mueve, un campo magnético aplicado sobre una brújula realiza trabajo cuando la aguja rota para alinearse con el campo y un par motor realiza trabajo cuando el árbol de salida gira más rápido. Puede decirse que el trabajo es un modo macroscópico de intercambio de energía en la medida de que tanto las fuerzas generalizadas como los desplazamientos generalizados son magnitudes agregadas, macroscópicas.
El calor es lo que queda cuando ya se ha tenido en cuenta el trabajo. Es una forma de intercambio de energía microscópica en la medida de que afecta directamente a las fluctuaciones de las partículas constituyentes del sistema alrededor del estado promedio que da lugar a las magnitudes agregadas macroscópicas afectadas por el trabajo.
El lenguaje es engañoso. A pesar de que un objeto caliente tiene una temperatura elevada, el calor no es la temperatura. De igual manera, el trabajo no es la energía de un sistema. Volvemos a lo indicado en el párrafo inicial: el calor y el trabajo son magnitudes en tránsito, interacciones vistas a nivel energético.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/30/el-trabajo-y-el-calor-en-termodinamica/
El concepto de sistema abierto en termodinámica
2015-09-28
Igual que ayer hablamos sobre los sistemas termodinámicos cerrados, hoy vamos a hablar de los sistemas abiertos, que son su contrapartida. Un sistema abierto es una parte del universo que sí permite el intercambio de materia con su entorno. A falta de barreras completamente impenetrables, cualquier parcela del universo es en realidad un sistema abierto, aunque a menudo puede hacerse la aproximación de sistema cerrado. Ahora bien, aunque cualquier fragmento del universo es un sistema abierto si se hace un esfuerzo suficiente para atravesar sus fronteras, no es descabellado postular que el universo completo, por su parte, es un sistema cerrado a falta de evidencia de una comunicación con otros universos como en las historias de fantasía.
El conjunto de los sistemas abiertos es extremadamente general, pero hay algunos sistemas en los que el intercambio de materia con el exterior es tan sencillo que su estudio no es mucho más complicado que el de un sistema idéntico que tuviera la única peculiaridad de tener la frontera cerrada al intercambio de materia. Por ejemplo, dentro de un nivel de aproximación excelente, el típico motor de combustión interna se deja analizar con una ley de entrada y salida de gases que sigue una relación algebraica con el punto de trabajo del motor.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/28/el-concepto-de-sistema-abierto-en-termodinamica/
El concepto de sistema cerrado en termodinámica
2015-09-27
En termodinámica se habla a menudo de sistemas cerrados. Un sistema cerrado es una parte del universo que tiene una característica muy especial: no intercambia materia con sus alrededores. Puede intercambiar energía, pero la materia no atraviesa sus fronteras.
En sistemas clásicos no relativistas, la materia puede hacer de todo; en concreto, puede cambiar sus propiedades mediante reacciones químicas. Ahora bien, en un sistema cerrado, la cantidad de materia no cambia ya que no hay intercambio con el exterior, con lo que la masa de cada especie atómica permanece constante. Esto no es del todo cierto, pero se trata de una aproximación excelente: aunque la masa de la materia realmente varía al producirse una reacción química, la corrección, que es de naturaleza relativista, es insignificante. La descripción se complica si hay que tener en ciertos fenómenos cuánticos (como la desintegración radiactiva) y relativistas.
La noción del sistema cerrado es importante tanto por aproximar numerosos casos prácticos como por su utilidad a la hora de definir algunos términos y algunos principios de la termodinámica.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/27/el-concepto-de-sistema-cerrado-en-termodinamica/
Breve apunte sobre las emisiones de óxidos de nitrógeno, las trampas y las prestaciones
2015-09-26
Los motores de combustión interna que mueven el grueso de los vehículos que circulan sobre la faz de la Tierra funcionan a base de quemar hidrocarburos con el óxigeno presente en la atmósfera. Los productos típicos de esta combustión son dióxido de carbono y agua (causantes del efecto invernadero), pero también emiten otras sustancias, algunas de ellas de efectos nocivos. Entre las sustancias peligrosas se encuentran los óxidos de nitrógeno («NOx», mayormente NO y NO2), que causan daños directos a la salud humana y también causan daños ambientales indirectos. La producción de estos óxidos de nitrógeno es consecuencia de usar aire como fuente de oxígeno para la combustión: buena parte del aire es nitrógeno molecular que, a las altas temperaturas alcanzadas durante al quemar (oxidar) el combustible principal del motor, también se oxida. La producción de óxidos de nitrógeno crece más y más deprisa conforme se aumenta la temperatura.
Los motores diésel tienen temperaturas y presiones de funcionamiento lo bastante elevadas como para que la producción de óxidos de nitrógeno sea un problema. Hay dos mecanismos fundamentales para reducir la emisión de óxidos de nitrógeno a la atmósfera por parte de un vehículo con motor diésel: reducir la temperatura y la presión alcanzadas durante la combustión y usar conversores catalíticos para reducir los óxidos de nitrógeno y convertirlos en sustancias menos nocivas (oxígeno molecular y nitrógeno molecular). Ambos mecanismos se encuentran con límites prácticos, naturalmente, pero han permitido reducir muy notablemente las emisiones de óxidos de nitrógeno de los vehículos con motor diésel. La regulación del proceso de combustión es especialmente jugosa debido a que hay varias formas de controlar dentro de razonablemente amplios y con variaciones aplicadas en tiempo real en respuesta a las necesidades dadas en cada momento. Ahora bien, no es algo que salga gratis: aunque las mejoras tecnológicas han venido frecuentemente acompañadas de reducciones en el consumo de combustible y reducciones en las emisiones, cuando la tecnología es fija, llega un momento en el que bajar la presión y la temperatura en la combustión disminuye la potencia de salida del motor con un consumo dado (aumenta el consumo necesario para dar una cierta potencia) e incluso se limita la potencia máxima alcanzable.
No es inaudito que en los ensayos de certificación del cumplimiento de la normativa de emisiones los fabricantes de automóviles jueguen con el funcionamiento de sus nuevos vehículos para conseguir medidas que poco se parecen a las que aparecen en condiciones de uso cotidianas. Un truco aplicado en los coches diésel que ha alcanzado mucha visibilidad estos días consiste en modificar al vuelo las condiciones de la combustión cuando la centralita de control detecta que se está produciendo un ensayo de certificación de emisiones. Como hemos visto, estas modificaciones empeoran las prestaciones del motor, así que la centralita reasigna los parámetros operativos cuando determina que no está en medio de un ensayo, lo que deja unas prestaciones atractivas para los posibles compradores de automóviles, pero aumenta las emisiones de óxidos de nitrógeno muy por encima de los límites establecidos por la normativa. Los dispositivos que hacen posible este truco son conocidos en la normativa estadounidense como «defeat devices» y están prohibidos, de ahí el problema en el que se ha metido un gigante de la automoción al ser pillado aplicando el truco.
Categorías: Miscelánea
Vocabulario aeroespacial (20): «semiala»
2015-09-22
El típico avión monoplano tiene un ala, no dos. Entonces, ¿cómo llaman los ingenieros aeronáuticos a cada una de las dos protrusiones que sobresalen a ambos lados del fuselaje y que proporcionan la fuerza de sustentación? Se llaman «semialas»: cada una de las dos mitades (izquierda y derecha o de babor y de estribor) que salen al cortar el ala por el plano de simetría.

Esquema de las semialas de un avión.
Categorías: Aeroespacio, Lingüística
Permalink: https://sgcg.es/articulos/2015/09/22/vocabulario-aeroespacial-20-semiala/
Las alas o el ala de un avión monoplano
2015-09-21
Aunque en el lenguaje coloquial se dice a menudo que un avión
monoplano tiene dos alas
, los aviones monoplanos tienen, por lo
general y en términos estructurales, un ala principal y no dos.
Aunque parece que salen dos alas diferenciadas del fuselaje, una a
cada lado, en realidad solamente hay un ala, una sola estructura que
atraviesa el interior del fuselaje. Si el ala estuviera interrumpida
al llegar al fuselaje, de modo que estructuralmente hubiera dos alas,
haría falta reforzar considerablemente la zona del encastre para
resistir las elevadas cargas transmitidas (hay que recordar que el ala
soporta prácticamente todo el peso de un avión en vuelo), ya que el
diseño típico de un fuselaje no se presta a resistir los esfuerzos
importantes de flexión local que se producirían. Al menos en un
contexto técnico, el ingeniero aeronáutico reconoce que es
generalmente incorrecto hablar de dos alas cuando el avión es
monoplano.
Categorías: Aeroespacio
Permalink: https://sgcg.es/articulos/2015/09/21/las-alas-o-el-ala-de-un-avion-monoplano/
Luneta para el mini torno de madera DB 250
2015-09-19
Tengo un mini torno de madera modelo DB 250 del fabricante Proxxon. Me gusta porque ocupa poco espacio. A veces, echo en falta una luneta para dar apoyo adicional a piezas alargadas. He decidido hacerme una. Antes de intentar algo bien rígido con aluminio o acero, he fabricado una prueba de concepto en ABS con mi vieja y temperamental Thing-o-Matic. Están todas las piezas necesarias salvo el tornillo de sujeción con su tuerca; para las pruebas voy a usar los del cabezal móvil.
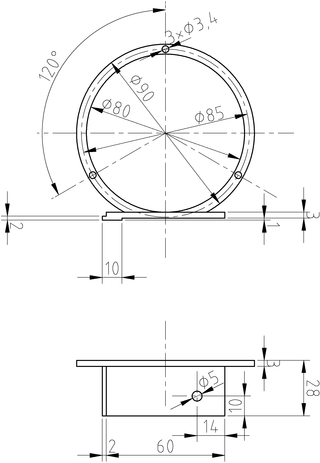
Dimensiones (en milímetros) del cuerpo principal de la luneta.
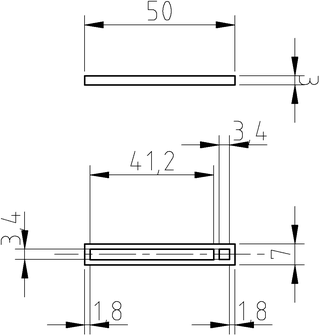
Dimensiones (en milímetros) de los brazos de la luneta.
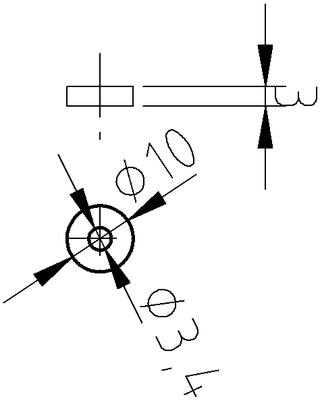
Dimensiones (en milímetros) de las ruedas de la luneta.

Fabricando la luneta.

La luneta montada.

La luneta en acción.
Parece que el prototipo funciona no demasiado mal para lo flexible que es el material y lo delgadas que son las secciones. Un poco de trabajo con él me servirá para plantear la versión definitiva, que probablemente será de aluminio.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/09/19/luneta-para-el-mini-torno-de-madera-db-250-1/
Maldita difracción o cómo esos megapíxeles tienen un límite
2015-09-18
En una cámara fotográfica convencional, aumentar la resolución del sensor (dentro de cierto rango) permite obtener imágenes más detalladas. La resolución de la imagen puede estar limitada, no obstante, por la calidad de la óptica y no por la propia resolución del sensor: si el objetivo tiene astigmatismo, por ejemplo, de manera que las imágenes siempre salen borrosas, un sensor de alta resolución no ayuda en principio.
Hay otra limitación a la resolución de las imágenes obtenidas por una cámara fotográfica convencional incluso cuando se usa una lente perfecta, libre de defectos. Esta limitación se debe a la naturaleza ondulatoria de la luz. Al entrar por el iris del objetivo, las ondas luminosas se difractan y se forma un patrón de interferencia en el sensor. Una fuente luminosa puntual (como una estrella distante que a simple vista es como un puntito de luz), en vez de producir un punto minúsculo en el plano de la imagen, produce un patrón similar a un disco rodeado de anillos concéntricos de luminosidad decreciente. Este patrón es lo que se conoce como disco de Airy y tiene un aspecto similar al de la siguiente figura:
![]()
Patrón provocado por la difracción.
La naturaleza ondulatoria de la luz conspira con la apertura finita del objetivo para provocar que las imágenes salgan siempre ligeramente borrosas, así que la resolución está limitada. Para luz con longitud de onda λ y con un diámetro de apertura del iris D, es difícil distinguir dos objetos si se encuentran separados un ángulo más pequeño que
1,22 λ ⁄ D.
Esto es lo que se conoce como el criterio de Rayleigh. Si la separación s entre los centros de dos píxeles contiguos en el sensor de una cámara digital es menor que la correspondiente a este ángulo, la resolución está limitada no por el sensor, sino por la difracción en el objetivo. Con una distancia focal f, la distancia angular entre dos píxeles queda bien aproximada por la fracción
s ⁄ f.
Por lo tanto, el criterio de Rayleigh establece que los puntos de luz recogidos por dos píxeles continuos se confunden cuando se cumple que
s < 1,22 λ (f ⁄ D).
La cantidad entre paréntesis es el número f que fija la apertura.
Veamos un ejemplo de lo expuesto: el caso de un sensor no especialmente pequeño, pero con una densidad de píxeles muy elevada. Recientemente, un gran fabricante de productos fotográficos anunció el desarrollo de un sensor de tamaño APS-H con una resolución de 19580 píxeles por 12600 píxeles. Un sensor de tamaño APS-H mide unos 29,2 mm por 20,2 mm. De estos números se deduce que la separación entre los centros de píxeles contiguos es, aproximadamente, s ≈ 1,5 µm. Según el criterio de Rayleigh, la resolución de la imagen está limitada por la difracción en el objetivo y no por el sensor (se «desperdicia» la alta densidad de píxeles del sensor) cuando el número f es mayor que 3,1 con luz violeta (con longitud de onda λ ≈ 400 nm) o incluso mayor que 1,8 con luz roja (con longitud de onda λ ≈ 700 nm). Esto no implica que la elevada resolución del sensor se haga completamente inútil nada más superar estos números f, pero sí indica que falta una lente rápida (con un número f pequeño) para obtener directamente imágenes con los detalles más finos que puede capturar un sensor con tan elevada densidad de píxeles.
En ciertas circunstancias, hay maneras de superar las limitaciones impuestas por la difracción. Consisten en usar técnicas de iluminación y captura de la imagen especiales o en realizar ciertos tratamientos de postproceso.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/18/maldita-difraccion-o-como-esos-megapixeles-tienen-un-limite/
Kiloartículo
2015-09-13
Este artículo es el milésimo: el kiloartículo. ¡Han pasado 2324 días desde que comenzó esta aventura! A lo largo de estos años, este sitio ha servido para compartir con amigos, familiares e incautos lectores montones de ideas, proyectos, reportajes fotográficos, contenido didáctico, dibujitos y muchas otras cosas. Esta página web personal, humilde como es, me ha provocado muchas satisfacciones.

Hoy estamos de celebración.
En estos tiempos en los que casi todo el contenido personal pasa por grandes plataformas corporativas, pensé que era bonito e interesante mantener el «viejo» arte de autopublicar una página personal con herramientas propias. La idea se convirtió en un proyecto con forma: una página entre tantísimas, pero la mía, al fin y al cabo. Poquito a poco y casi sin darme cuenta, esto ha crecido hasta el millar de artículos.

Igual que una planta que crece con el riego y los cuidados
adecuados, una página web personal vive de un goteo incesante de
nuevas ideas.
Mil artículos dan para hablar de muchas cuestiones diferentes. Como este sitio no tiene un tema fijo y bien definido, sino que es mi pequeña ventana al mundo, esas muchas cuestiones diferentes son realmente muchas y diferentes. Este sitio está organizado como la típica bitácora o «weblog», pero no tiene publicidad y no trata de dar un producto perfectamente dirigido a un pequeño nicho del mercado de los lectores como hacen otras bitácoras (lo que no es algo malo), así que puedo permitirme el lujo de publicar lo que me apetece en cada momento. Al placer de rascar el figurado picor de la difusión de ideas se añade que, de vez en cuando, algún incauto lector encuentra un artículo que es de su interés y agrado y me escribe para comentármelo, para sugerir nuevos temas o para pedirme ayuda con proyectos relacionados con lo leído; esto siempre es agradable.
Es bonito compartir.
Incauto lector, igual que hice en el hectoartículo hace casi 6 años, te invito a volver siempre que quieras. ¡Nos divertiremos! Recuerda que puedes mandar tus opiniones, comentarios y sugerencias por correo electrónico.

¡Fiesta!
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2015/09/13/kiloarticulo/
Tensiones o esfuerzos mecánicos (12)
2015-09-12
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hay varias maneras de resumir las características de este tensor; algunas, como el elipsoide de Lamé, son representaciones geométricas. El artículo de hoy trata sobre los círculos de Mohr, que son otra representación geométrica que además permite el cálculo gráfico de la componente normal y la componente tangencial del vector tensión.
Los círculos de Mohr
Los círculos de Mohr son una representación de los posibles valores que pueden adoptar la tensión normal y la tensión cortante al variar la dirección de medida.
Trabajemos en ejes principales con la numeración escogida tal que las tensiones principales están ordenadas de la siguiente manera:
σ1 ≥ σ2 ≥ σ3.
Medido en una dirección cualquiera (actuando sobre un plano cualquiera) dada por el vector normal n, el vector tensión t tiene componentes
ti = σi ni, i ∈ {1,2,3}.
El cuadrado del módulo de este vector tensión es
t ⋅ t = (σ1)2 (n1)2 + (σ2)2 (n2)2 + (σ3)2 (n3)2.
El vector normal se descompone en una componente normal al plano de medida (paralela a la dirección de medida) de magnitud σ (la tensión normal) y una componente tangente al plano de medida (perpendicular a la dirección de medida) de magnitud τ (la tensión tangencial). La tensión normal sale, por lo tanto, de proyectar sobre el vector normal:
σ ≡ t ⋅ n = σ1 (n1)2 + σ2 (n2)2 + σ3 (n3)2.
La magnitud del vector tensión está relacionada con la tensión normal y la tensión tangencial mediante el Pitágoras:
t ⋅ t = σ2 + τ2.
Tanto esta ecuación del teorema de Pitágoras como la primera del cuadrado del módulo del vector tensión son lineales en los cuadrados de las componentes del vector normal. Otra ecuación con la misma forma es la que establece que el vector normal tiene, por definición, módulo unitario:
(n1)2 + (n2)2 + (n3)2 = 1.
Asumamos ahora que las tensiones principales son diferentes entre sí. El sistema de tres ecuaciones queda diagonalizado de la siguiente manera:
(σ1−σ2) (σ1−σ3) (n1)2 = (σ−σ2) (σ−σ3) + τ2;
(σ2−σ1) (σ2−σ3) (n2)2 = (σ−σ3) (σ−σ1) + τ2;
(σ3−σ1) (σ3−σ2) (n3)2 = (σ−σ1) (σ−σ2) + τ2.
Estas ecuaciones se prestan a una interpretación geométrica muy interesante en el plano (σ,τ). Hay varias conclusiones que podemos extraer: por una parte, las tensiones normales y tangenciales ocupan el lugar geométrico interior a una circunferencia grande y exterior a dos circunferencias pequeñas (los círculos de Mohr); por otra parte, es posible usar las propiedades de la potencia de un punto respecto a una circunferencia para determinar gráficamente la tensión normal y la tensión tangencial en una dirección cualquiera.
Lugar geométrico de las tensiones
Debido al orden de las tensiones principales y a que los cuadrados de las componentes de la dirección normal son positivos, salen las siguientes inecuaciones que fijan el lugar geométrico de las tensiones normales y tangenciales:
(σ−σ2) (σ−σ3) + τ2 ≥ 0;
(σ−σ3) (σ−σ1) + τ2 ≤ 0;
(σ−σ1) (σ−σ2) + τ2 ≥ 0.
Estas tres inecuaciones determinan los siguientes lugares geométricos:
- El exterior de un círculo centrado en el punto σ = (σ3+σ2) ⁄ 2, τ = 0 y de radio σ2−σ3 (un círculo de radio pequeño).
- El interior de un círculo centrado en el punto σ = (σ3+σ1) ⁄ 2, τ = 0 y de radio σ1−σ3 (un círculo de radio grande).
- El exterior de un círculo centrado en el punto σ = (σ1+σ2) ⁄ 2, τ = 0 y de radio σ1−σ2 (un círculo de radio pequeño).
Estos círculos son los círculos de Mohr. Los puntos en el plano de las tensiones se encuentran en la región que es a la vez interior al círculo grande y exterior a los círculos pequeños.
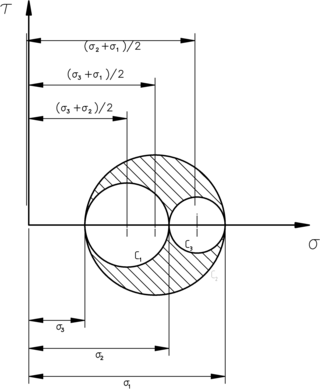
Círculos de Mohr. Las tensiones pueden adoptar valores en el área
rayada.
Cálculo gráfico de las tensiones
El sistema de ecuaciones diagonalizado es, además, el de la potencia de un punto con respecto a los círculos (las circunferencias) de Mohr. En concreto, el lado derecho de cada ecuación es la potencia respecto a la circunferencia correspondiente. El lado izquierdo de cada ecuación está en forma de producto de dos diferencias y el cuadrado de un coseno director, análogo al producto de dos distancias que es la potencia de un punto respecto a una circunferencia. Basta construir estas distancias. Las siguientes figuras muestran construcciones que cumplen las respectivas ecuaciones de la potencia:
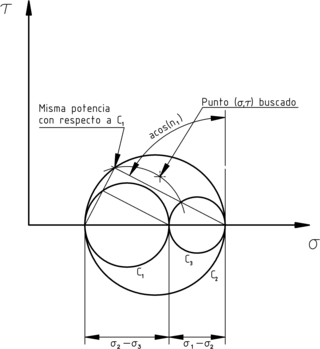
Potencia relativa a la circunferencia 1.
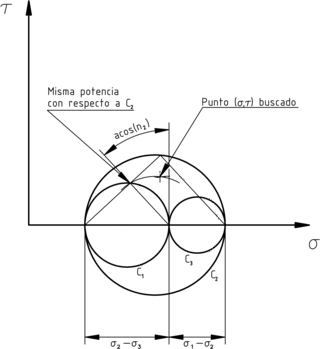
Potencia relativa a la circunferencia 2. También puede hacerse la
construcción análoga en sentido horario.
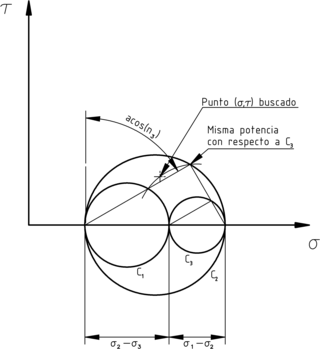
Potencia relativa a la circunferencia 3.
Basta usar 2 de estas construcciones para calcular gráficamente la tensión normal y la tensión tangencial cuando se conocen las componentes del vector normal:
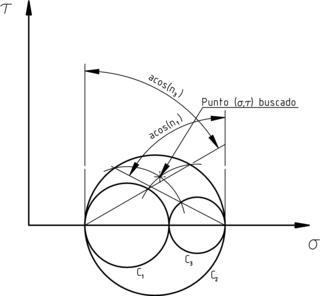
Cálculo gráfico de la descomposición del vector tensión. En cada
punto σ
= σi, τ = 0 se traza
una línea desviada de la vertical el
ángulo acos(ni) y
seguidamente se traza un arco concéntrico con la
circunferencia Ci que
corte la intersección de la línea con las otras circunferencias. El
punto buscado es la intersección de los arcos trazados.
El mismo principio permite calcular gráficamente las direcciones normales correspondientes a un punto en el plano (σ,τ).
Máxima tensión tangencial
De la construcción de los círculos de Mohr se deduce que la máxima tensión tangencial o cortante es igual al radio del círculo mayor:
τmáx = σ1−σ4.
Del cálculo gráfico se deduce que las componentes del vector normal son
n1,τmáx = cos(π ⁄ 4) = (√2) ⁄ 2;
n2,τmáx = cos(π ⁄ 2) = 0;
n3,τmáx = cos(π ⁄ 4) = (√2) ⁄ 2.
Tensiones principales iguales
Cuando las 3 tensiones principales son iguales, los círculos de Mohr colapsan en un punto. Es un estado de tensión hidrostática pura.
Cuando σ1 = σ2 ≠ σ3, el lugar geométrico de las tensiones se limita a la circunferencia mayor C2.
Cuando σ3 = σ2 ≠ σ1, el lugar geométrico de las tensiones es el interior completo de la circunferencia mayor C2.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/12/tensiones-o-esfuerzos-mecanicos-12/
Tensiones o esfuerzos mecánicos (11)
2015-09-07
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hay varias maneras de resumir las características de este tensor; ya vimos tres de ellas: las tensiones principales, los invariantes y las tensiones octaédricas. Hoy vamos a ver otra representación que, como las anteriores, es característica de las matrices simétricas: el elipsoide de Lamé.
El elipsoide de Lamé
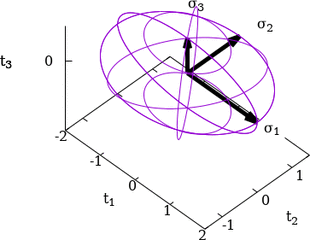
Elipsoide de Lamé: el lugar geométrico de los vectores tensión
generados por un tensor de tensiones.
Sabemos que el vector tensión en un punto dado resulta de una aplicación lineal sobre la dirección de medida. Si tomamos como triedro de referencia el definido por los ejes principales correspondientes a las tensiones principales σ1, σ2 y σ3, las componentes t1, t2 y t3 del vector tensión medido en la dirección con dirección normal de componentes n1, n2 y n3 son las siguientes:
t1 = σ1 n1;
t2 = σ2 n2;
t3 = σ3 n3.
Si conocemos las componentes del vector tensión y las tensiones principales, podemos saber la dirección de medida:
n1 = t1 ⁄ σ1;
n2 = t2 ⁄ σ2;
n3 = t3 ⁄ σ3.
La dirección normal de medida, por definición, está normalizada:
(n1)2 + (n2)2 + (n3)2 = 1.
Si combinamos las últimas expresiones, obtenemos la siguiente relación:
(t1 ⁄ σ1)2 + (t2 ⁄ σ2)2 + (t3 ⁄ σ3)2 = 1.
Esta ecuación es la de un elipsoide en el espacio de las componentes de los vectores tensión: el elipsoide de Lamé. Con unas tensiones principales dadas, el vector tensión está restringido a adoptar valores en el correspondiente elipsoide de Lamé.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/07/tensiones-o-esfuerzos-mecanicos-11/
