Agosto de 2012
Calendario de artículos de de 2012
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
Las proezas físicas de Superman (6): capaz de doblar acero con las manos
2012-08-29
Continúa la serie de artículos sobre la fuerza de Superman durante sus primeros años de publicación. Hoy veremos qué fuerza tenía que hacer para doblar una viga de acero con las manos desnudas (tal como decía la entradilla del número 9 de Action Comics).
Un modelo elemental para la deformación plástica de una viga
Al flexionar una viga de acero, surge una distribución de tensiones en las secciones transversales; esta distribución de tensiones (esfuerzos internos que mantienen el material cohesionado) compensa el momento flector aplicado sobre la viga (una carga externa) del mismo modo que al estar de pie sobre el suelo, el propio suelo se comprime en menor o mayor medida y aparece una presión que compensa nuestro propio peso e impide que nos hundamos. Si doblamos la viga hacia abajo, la parte superior de la sección estará traccionada (tendemos a separar sus átomos) y la parte inferior estará comprimida (tendemos a unir sus átomos).
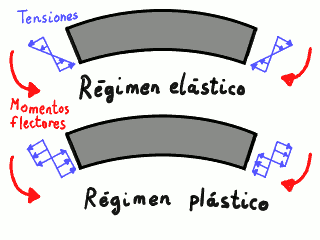
Distribución de tensiones y cargas aplicadas en una viga.
Podemos asumir que un material tiene dos maneras de deformarse:
- elásticamente
- cuando el material recupera su forma original tras retirar la carga;
- plásticamente
- cuando el material se queda deformado permanentemente incluso tras retirar la carga.
En el régimen elástico, hay que aumentar la tensión para hacer que la deformación. A partir de cierto punto, la elasticidad del material ya no puede más y las deformaciones plásticas se hacen apreciables. La tensión a partir de la que comienza el régimen plástico es el límite elástico, σy. A veces, el límite elástico no está bien definido, pero no es el caso que nos interesa ahora. En un material perfectamente plástico, sería posible deformar el material sin aumentar apreciablemente la carga. Aunque los materiales perfectamente plásticos son una entelequia, el acero estructural sí se parece mucho a uno tras superar el límite elástico, ya que la tensión tiene que crecer muy poquito (comparada con la que ya estaba establecida) para incrementar la deformación plástica.
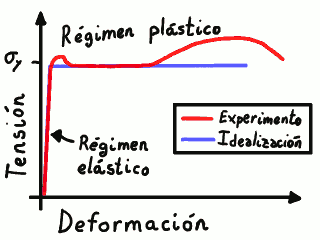
Curva de tensión frente a deformación de un acero estructural.
Hay un quiebro (el límite elástico) y a partir de él las deformaciones
crecen mucho con la tensión. La curva roja representa los datos del
acero real, mientras que la curva azul representa el modelo de material
elástico lineal y perfectamente plástico.
Cuando Superman dobla una viga, ésta se deforma plásticamente.
Las tensiones que aparecen en las secciones transversales son como
las del régimen plástico que aparece en la figura de las tensiones
y las cargas de más arriba: la parte que trabaja a tracción tiene
una tensión igual al límite elástico, mientras que la parte
que se encuentra comprimida tiene una tensión igual a menos el
límite elástico. Estas tensiones tienen que equilibrar el momento
flector que obliga a doblar la viga. De aplicar el equilibrio
con este modelo, queda una relación muy sencilla entre el momento
flector M, el límite elástico
σy y la
geometría de la sección, resumida en un parámetro conocido como el
módulo plástico de la sección, Z:
M = σy Z.
Superman dobla la viga
Para doblar la viga, Superman la sujeta con los brazos sobre su
cabeza y hace una fuerza hacia abajo. La cabeza hace de punto de
apoyo y la increíble fuerza aplicada. Cada uno de los brazos ejerce
una fuerza F a una distancia l de la cabeza. El momento flector es,
evidentemente,
M = F l.
Todo esto aparece representado en la siguiente figura:
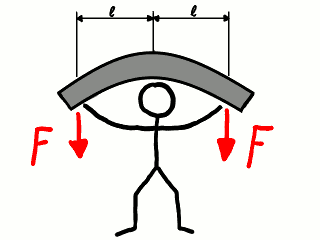
Acto de doblar una viga con las manos.
Hay muchos tipos de acero y cada uno tiene su límite elástico σy correspondiente. Podemos elegir uno estructural bastante típico como el ASTM A36, uno que se usa mucho en Estados Unidos y que tiene un límite elástico de 250 GPa. La curva del ensayo de tracción del A36 se parece mucho a la de la figura de arriba de la tensión frente a la deformación.
Vimos anteriormente que también tenemos que conocer el módulo plástico de la sección transversal de la viga, Z. Éste depende de la geometría de la sección y de la dirección de la carga. A sabiendas de que buscamos verificar la fuerza que determinamos en anteriores artículos de esta serie, vamos a suponer que la sección es una W8×67 según la norma ASTM A6, una viga en I cuyo módulo plástico según la dirección más costosa (pues Superman está haciendo una buena demostración de fuerza) es igual a 1149 cm3.
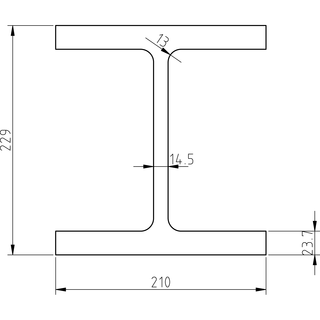
Aproximación de la sección de la viga W8×67 según la norma
ASTM A6 (o, más bien, una viga W200×100 de la norma ASTM A6M,
que es equivalente a la ASTM A6, pero con dimensiones de acuerdo
con el Sistema Internacional).
Finalmente, tenemos que saber la distancia l al punto de apoyo a la que Superman aplica la fuerza. Una viga de acero es algo formidable, así que diremos que separa sus brazos en toda su extensión hasta aproximadamente 1 m de distancia del punto de apoyo.
Ya tenemos todos los números: σy = 250 GPa,
Z = 1149 cm3
y l = 1 m. Si juntamos
la ecuación de equilibrio
M = σy Z
y la definición del momento
M = F l,
queda que la fuerza es de unos 300 kN, que es lo que estábamos buscando.
Esta vez, los datos están forzados para cuadrar con lo esperado,
pero estos datos son perfectamente razonables.
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más rápido que una bala!
- ¡Más poderoso que una locomotora!
- ¡Capaz de saltar sobre edificios altos!
- ¡Capaz de levantar grandes pesos!
- ¡Capaz de liberarse de una cadena de acero!
Las proezas físicas de Superman (5): capaz de liberarse de una cadena de acero
2012-08-28
Continúa la serie de artículos sobre la fuerza de Superman durante sus primeros años de publicación. Hoy veremos qué fuerza tenía que hacer para liberarse de una cadena de acero tal como aparecía en la contraportada del primer número de Superman (1939).
Cómo romper una cadena
Superman se encuentra aparentemente inmovilizado con una cadena que rodea su torso y sus brazos. Sin duda, una persona corriente tendría serios problemas para escapar, pero Superman es asombrosamente fuerte y sólo tiene que sacar pecho y hacer fuerza con los brazos para traccionar los eslabones de la cadena hasta el punto de romperlos y quedar libre.
Vamos a hacernos una idea simplificada del mecanismo mediante el que puede romperse la cadena que tenía atrapado a Superman. Al tirar de la cadena, se produce una tensión que mantiene unido el material, pero esta tensión no puede la tensión no puede crecer indefinidamente, sino que tiene un valor máximo: la resistencia a la tracción del material. Si se exige una tensión mayor, el material ya no puede mantenerse cohesionado y se fractura.
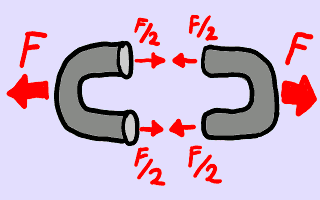
Fuerzas en un eslabón.
Los eslabones tienen a menudo una sección circular. Los del
dibujo pueden tener secciones de 1 cm
de diámetro. El área de la sección (a la que llamaremos
A) es de unos 80 mm2. La fuerza que
aguanta una sección antes de romperse será igual al producto
de la tensión σ a la que
está sometida y su área A. Un
eslabón es topológicamente un toro y tiene dos secciones trabajando
a tracción en paralelo, así que la fuerza de tracción F que resiste el eslabón es el doble
de la fuerza que resiste una sola sección:
F = 2 σ A.
Los eslabones se rompen cuando la tensión σ alcanza la resistencia a la
tracción del material. Sin duda, los captores de Superman sabían
que trataban con un tipo extraordinario, así que no se andaron con
chiquitas y usaron un excelente acero inoxidable al cromo-níquel
18/8 endurecido del que se producía con una resistencia de incluso
unos 2 GPa en 1939. Así que tomamos
σ = 2 GPa y
A = 80 mm2.
La fuerza que hace Superman para soltarse es, por lo tanto,
F = 2 σ A = 2 ⋅ 2 GPa ⋅ 80 mm2 ≈ 300 kN.
¡Como siempre, el Superman de comienzos de la Edad de Oro podía
hacer una fuerza de 300 kN con cualquier
parte de su cuerpo!
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más rápido que una bala!
- ¡Más poderoso que una locomotora!
- ¡Capaz de saltar sobre edificios altos!
- ¡Capaz de levantar grandes pesos!
- ¡Capaz de doblar vigas de acero con las manos!
RIP Neil Armstrong
2012-08-26

Neil Armstrong, primer ser humano en pisar la Luna y hombre extraordinario, falleció ayer 25 de agosto de 2012 debido a complicaciones producidas tras una intervención de cirugía cardiovascular. Como homenaje, su familia nos deja estas palabras:
For those who may ask what they can do to honor Neil, we have a simple request. Honor his example of service, accomplishment and modesty, and the next time you walk outside on a clear night and see the moon smiling down at you, think of Neil Armstrong and give him a wink.
Para quienes se pregunten qué pueden hacer para honrar a Neil, tenemos una sencilla petición. Honrad su ejemplo de servicio, logros y modestia y la próxima vez que paseéis en una noche clara y veáis a la Luna sonriéndoos, pensad en Neil Armstrong y guiñadle el ojo.
Categorías: Actualidad, Aeroespacio
Permalink: https://sgcg.es/articulos/2012/08/26/rip-neil-armstrong/
Las proezas físicas de Superman (4): capaz de levantar grandes pesos
2012-08-25
Continúa la serie de artículos sobre la fuerza de Superman durante sus primeros años de publicación. Hoy veremos cuánto peso se mostraba capaz de levantar sobre su cabeza.
¡Levantar un coche!
En el primer número de Action Comics, Superman levanta (¡con un solo brazo!) y zarandea un coche con cuatro ocupantes. Los coches como el de la viñeta tenían masas de alrededor de 1000 kg, así que Superman levantaba 10 kN cómodamente. ¡Eso es poco comparado con lo que podemos llegar a ver más adelante!
¡Levantar un elefante!
En el número 7 de Action Comics, Superman se une a un circo y hace llamativas demostraciones de fuerza. Llegó a levantar un confundido elefante con el brazo derecho. El elefante de la viñeta no es muy grande; su masa quizá no supera los 3000 kg. Esto es más que un coche, no obstante.
¡Levantar un tranvía!
Era habitual que la primera viñeta del cómic mostrara al protagonista en acción. El mismo número 7 de Action Comics mostraba a Superman sosteniendo un tranvía cómodamente sobre su cabeza. El tranvía parece un Birney corto. El Birney tenía una tara de 8000 kg y podía llevar 32 pasajeros, lo que daba una masa típica entre 10000 kg y 11000 kg con el vehículo lleno. El Birney tenía nueve ventanillas laterales, mientras que el tranvía de la viñeta sólo muestra siete; no es descabellado aproximar la masa del tranvía de la viñeta, por lo tanto, como las siete novenas partes de la masa del Birney lleno (es decir, unos 8000 kg). Mantener en el aire el tranvía supondría ejercer unos 80 kN.
¡Levantar un tranvía rápidamente!
Superman no tarda un tiempo infinito en levantar el tranvía sobre su cabeza, así que tendrá que imprimir a su carga una aceleración considerable. Si conocemos el tiempo que tarda Superman en poner el tranvía sobre su cabeza, podemos deducir la aceleración promedio. Superman parece cómodo en la viñeta y podemos suponer que levantó el tranvía rápidamente. Hay varias estrategias para levantar un peso, pero una consiste en acelerarlo hasta la mitad del camino y luego dejar que su propio peso lo frene; de esta manera, la primera parte del levantamiento consiste en ejercer una fuerza equivalente al doble del peso, mientras que en la segunda parte no se hace fuerza y se deja que la gravedad actúe sola. Con este planteamiento, la fuerza sería de unos 160 kN. Como la distancia a la que Superman eleva el tranvía es de 2 m (la propia estatura del héroe), el tiempo de elevación es el doble del que tardaría el peso en caer desde 1 m (la mitad de altura): 0,9 s, un tiempo perfectamente razonable.
Superman puede elevar el tranvía más deprisa si en la segunda mitad de la elevación no se limita a dejar que la gravedad frene el peso, sino que además él mismo pone algo de esfuerzo. El efecto buscado es el de antes: dar una aceleración constante hacia arriba durante la primera mitad del camino y la misma aceleración hacia abajo durante la segunda mitad del camino. En anteriores artículos, vimos que Superman era capaz de ejercer 300 kN cómodamente de diferentes maneras. Casi podríamos decir que aquel Superman inicial era el hombre de los 300 kN. Esta fuerza es aproximadamente el cuádruple del peso del tranvía y si Superman ejerciera toda esta fuerza durante la mitad del camino, la aceleración sería aproximadamente igual al triple de la gravitatoria (como la fuerza es cuatro veces el peso, una cuarta parte vence a la gravedad y tres cuartas partes imprimen aceleración). La elevación lleva el doble de tiempo que una caída desde 1 m de altura (la mitad del camino) al triple de la aceleración gravitatoria: 0,5 s. He estado levantando objetos sobre mi cabeza y tardo cosa de 0,5 s cómodamente, así que Superman, que también parece muy cómodo en la viñeta, podría tardar ese tiempo, con lo que estaría haciendo, como siempre, una fuerza 300 kN.
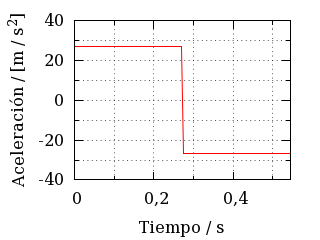
Aceleración vertical del tranvía cuando lo levanta Superman.
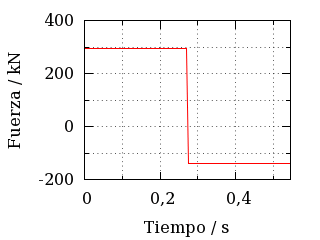
Fuerza ejercida por Superman cuando levanta el tranvía.
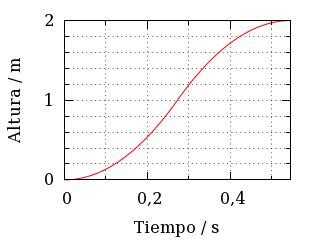
Altura a la que se encuentra el tranvía conforme Superman lo levanta.
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más rápido que una bala!
- ¡Más poderoso que una locomotora!
- ¡Capaz de saltar sobre edificios altos!
- ¡Capaz de liberarse de una cadena de acero!
- ¡Capaz de doblar vigas de acero con las manos!
Las proezas físicas de Superman (3): capaz de saltar sobre edificios altos
2012-08-23
Continúa la serie de artículos en la que medimos la fuerza que tenía Superman durante sus primeros años de publicación. Hoy vamos a calcular la fuerza que hacía al saltar por encima de edificios altos.
¿Cómo de alto es un edificio alto?
Debemos determinar la altura del edificio sobre el que Superman
podía pasar de un salto. El primer número de Action Comics
contiene la información buscada en la cuarta viñeta: Superman podía
saltar 300 m, sobrepasar un edificio
de veinte plantas
. Como los edificios de veinte plantas son mucho
más bajos que 300 m, se entiende que
la primera afirmación se refiere a un salto de longitud. Un edificio
de oficinas de veinte plantas puede medir unos 100 m, decámetro arriba o decámetro abajo.
La fuerza del salto
Vamos a suponer que el salto es casi perfectamente vertical (efectivamente vertical en lo que se refiere al cálculo) y que la resistencia aerodinámica es despreciable. Es fácil verificar a posteriori que el error cometido en la estimación es de unas centésimas partes, así que no merece la pena complicar las cuentas. Con estas hipótesis, la energía se conserva y el incremento de energía potencial gravitatoria desde el suelo hasta el punto más elevado del salto ha de venir del trabajo realizado por la fuerza ejercida durante el salto. Esta fuerza es aplicada hacia abajo con los pies sobre el suelo y a su vez la reacción del suelo (opuesta a la fuerza aplicada por los pies) empuja a Superman hacia arriba.

Salto sobre un edificio alto.
Antes de saltar, Superman tiene que agacharse un poco; durante la extensión de piernas y hasta que los pies pierden el contacto con el suelo y ya no se ejerce más fuerza, el centro de masas de Superman se desplaza una distancia l hacia arriba.
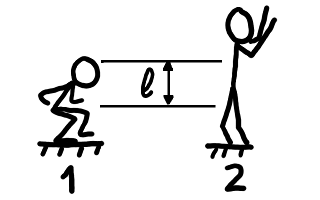
Desarrollo de un salto. El centro de masas se ha desplazado
una altura l entre la preparación (1)
y el despegue (2).
La fuerza aplicada varía durante el desarrollo del salto, así que trabajaremos con su valor F promediado a lo largo del desplazamiento l.
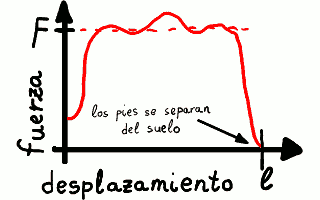
Variación de la fuerza aplicada durante el desarrollo de un salto.
El trabajo realizado es igual al producto de la fuerza promedio
y el desplazamiento, F l.
Este trabajo acaba convirtiéndose por completo en energía potencial
en el punto más alto de la trayectoria; el incremento de energía
potencial es igual al producto de la masa m,
la aceleración gravitatoria g y la
altura h. Queda, por lo tanto,
esta ecuación:
F l = m g h.
Vamos a asignar valores a las variables para poder despejar la fuerza:
- Al agacharse para preparar el salto, Superman no necesita ponerse a cuatro patas, sino que basta con que flexione las piernas un poco. Un valor adecuado para el desplazamiento l puede ser del entorno de 30 cm o quizá 40 cm.
- La masa m de Superman es de unos 100 kg.
- La aceleración gravitatoria g es próxima a 10 m ⁄ s2.
- La altura h del salto es de unos 100 m.
Con estos números, la fuerza promedio F con la que se impulsa Superman es de unos 300 kN. Es el mismo valor que vimos en los dos anteriores artículos.
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más rápido que una bala!
- ¡Más poderoso que una locomotora!
- ¡Capaz de levantar grandes pesos!
- ¡Capaz de liberarse de una cadena de acero!
- ¡Capaz de doblar vigas de acero con las manos!
Las proezas físicas de Superman (2): más poderoso que una locomotora
2012-08-22
Seguimos con nuestro repaso a las habilidades que tenía Superman durante sus primeros años de publicación.
Se decía que Superman era más poderoso que una locomotora (more powerful than a locomotive). Podemos interpretar esto de dos maneras diferentes:
- que podía ejercer una potencia superior a la de una locomotora;
- que podía ejercer más fuerza que una locomotora.
Tenemos entre manos dos conceptos diferentes.
La potencia de una locomotora
Un valor típico de la potencia máxima de una locomotora de tren de pasajeros de los años treinta y cuarenta del siglo XX está en 1 MW o 2 MW.
Los mercancías tienen a menudo locomotoras muy potentes. El Superman inicial pudo ver perfectamente locomotoras con una potencia de unos 7 MW. Los trenes de pasajeros podían tener locomotoras de entre 1 MW y 2 MW. Anteriormente vimos que Superman podía correr a unos 900 m ⁄ s y que para ello necesitaba vencer una resistencia aerodinámica de unos 300 kN. El producto de estos dos valores es la potencia necesaria para correr tan rápido mientras se vence la resistencia del aire y tiene un valor de 270 MW. Esto es incluso cien veces la potencia de una locomotora.
La fuerza tractora de una locomotora
Las locomotoras de vapor usadas en trenes de pasajeros y de mercancías de los años treinta y cuarenta del siglo XX daban fuerzas tractoras típicas de algún que otro centenar de kN. Una locomotora grande podía dar unos 300 kN, que es la fuerza que hacía Superman para vencer la resistencia aerodinámica al correr más rápido que una bala de rifle.
Parece que Superman era generalmente capaz de aplicar unos 300 kN.
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más rápido que una bala!
- ¡Capaz de saltar sobre edificios altos!
- ¡Capaz de levantar grandes pesos!
- ¡Capaz de liberarse de una cadena de acero!
- ¡Capaz de doblar vigas de acero con las manos!
Kelvin gramo
2012-08-18
La unidad de masa del Sistema Internacional es el kilogramo. El símbolo se escribe así: kg. Las dos letras van en minúsculas. Un error común consiste en escribir *Kg, algo que tiene un significado completamente diferente del deseado: el prefijo para «kilo» es «k», no «K», que significa "kelvin"; «Kg» significa "kelvin gramo", es decir, el producto de una temperatura y una masa. La distinción entre mayúsculas y minúsculas es fundamental. Veamos un recopilatorio de errores comunes:
- Kg
- kelvin gramo (temperatura multiplicada por masa).
- kG
- kilogauss (es decir, decitesla, campo magnético).
- KG
- kelvin gauss (temperatura multiplicada por campo magnético).
- kgr. y otras cosas igual de feas
- no todo el mundo tuvo la fortuna de recibir una educación adecuada en lo que se refiere a unidades de medida.
Categorías: Física, Lingüística
Permalink: https://sgcg.es/articulos/2012/08/18/kelvin-gramo/
Las proezas físicas de Superman (1): más rápido que una bala
2012-08-16
Superman es uno de los personajes más conocidos del mundo del cómic. Uno de los rasgos distintivos del hombre de acero es su espectacular fuerza sobrehumana. Ahora bien, esta tremenda fuerza ha variado mucho con el tiempo: el Superman de los años anteriores a Crisis en Tierras Infinitas, por ejemplo, era tan absurdamente poderoso que llegamos a verlo arrastrando hileras de planetas como si nada, mientras que el de los primeros años de Siegel y Shuster, aunque era un forzudo de cuidado, todavía no había llegado a tal nivel y era más bien comparable con campeones clásicos como Hércules. Hoy vamos a hacer una estimación de la fuerza que podía hacer este Superman primitivo al correr.
Más rápido que una bala
Decían que Superman era más rápido que una bala. ¿Cómo de rápido es eso? Pues depende de la bala, por supuesto. Para fijar ideas, supongamos una rapidez de 900 m ⁄ s, algo característico de una bala para rifle. Esto es Mach 2,6 en condiciones normales, por cierto.
En llano y en régimen estacionario (sin acelerar ni frenar), un corredor ha de ejercer una tracción que compense la resistencia aerodinámica. Si conocemos la resistencia aerodinámica de Superman a Mach 2,6 en condiciones normales, entonces tenemos una estimación de la fuerza que puede hacer el último hijo de Krypton al correr.
Hay un problemilla con todo esto: los datos de resistencia
aerodinámica de corredores en régimen supersónico no son
precisamente abundantes. A falta de una buena sesión de colourful
fluid dynamics, habrá que hacer una estimación a partir
de datos experimentales. La fuerza de resistencia es ésta:
(1 ⁄ 2) ρ S V2 CD.
En esta expresión:
- ρ es la densidad del aire (que tomaremos como 1,2 kg ⁄ m3 en condiciones normales).
- S es la superficie frontal de Superman en carrera. Estimo esta superficie en unos 0,5 m2 tras medir varias viñetas publicadas entre 1939 y 1940. La medida varía en torno a un 25 %.
- V es la rapidez (que dijimos que sería de unos 900 m ⁄ s).
- CD es el coeficiente de resistencia. Aquí está lo más difícil de conseguir. Tengo mi socorrido Hoerner a mano y hay unas cuantas curvas que vienen muy bien. Aunque Superman se inclina al correr, está muy próximo al suelo y forma algo que, corriente arriba, se parece más a un ladrillo que a una bala. Es una apuesta segura suponer que forma una enorme onda de choque normal desprendidísima y su coeficiente de resistencia se parece mucho al típico de cuerpos muy romos. Dejémoslo en 1,3, póngasele o quítesele 0,3. La incertidumbre es comparable a la de la superficie frontal.
Con todos estos números, la fuerza de resistencia queda en unos 300 kN. Eso es equivalente a levantar cientos de veces el propio peso y es consistente con otras proezas físicas del Superman de los primeros tiempos.
¿Qué nivel de poder es esto?
¡El nivel de poder (o la capacidad de ataque) es de Dragon Ball, no de Superman! El conocimiento popular (y el Scouter de Raditz, el malvado hermano de Son Goku) dice que un ser humano promedio tiene un nivel de poder de 5. Un hombre medio esprinta a unos 10 m ⁄ s y, de acuerdo de nuevo con el Hoerner, tiene en régimen subsónico bajo un producto del área frontal por el coeficiente de resistencia de en torno a 0,5 m2. La resistencia aerodinámica es, por lo tanto, de unos 30 N, lo que no parece mucho, pero hay que recordar que no es lo mismo esprintar que levantar un peso con los pies bien firmes en el suelo (entre otras cuestiones, al correr hay que acelerar las piernas y eso supone un esfuerzo que no estamos teniendo en cuenta pero que crece más o menos como la resistencia aerodinámica: con el cuadrado de la rapidez). Si suponemos que el grueso del esfuerzo se va en vencer a la resistencia aerodinámica y usamos una escala lineal para el nivel de poder, deducimos que Superman tiene una capacidad de al menos 10000. ¡Estos últimos números son extremadamente imprecisos!
Más artículos de esta serie
En esta serie vemos que el Superman de los primeros tiempos siempre ejercía una fuerza de 300 kN. Salen unos problemas de mecánica aplicada francamente sencillos y fáciles de resolver, pero quizá interesantes como material didáctico.
- ¡Más poderoso que una locomotora!
- ¡Capaz de saltar sobre edificios altos!
- ¡Capaz de levantar grandes pesos!
- ¡Capaz de liberarse de una cadena de acero!
- ¡Capaz de doblar vigas de acero con las manos!
Permalink: https://sgcg.es/articulos/2012/08/16/las-proezas-fisicas-de-superman-1-mas-rapido-que-una-bala/
Sobre el fusible de los puertos de entrada de la Sega Dreamcast
2012-08-11
Los puertos de entrada donde van enchufados los mandos de la videoconsola Sega Dreamcast están montados sobre una placa de circuito impreso en la que además van el piloto de encendido, el conector del ventilador, la pila recargable del reloj y un pequeño fusible axial que, visto de lejos, parece un resistor.

La flecha roja superpuesta señala el fusible,
el componente azul con cinco bandas de colores.
No se ve en la fotografía, pero en la placa aparece
la marca «F1» al lado del fusible.
Este fusible está entre una línea de 5 V y la alimentación de los mandos. Si salta, todos los mandos dejan de funcionar.
Circula información diversa sobre qué hacer para reemplazarlo:
- En algunos lugares indican que es posible usar resistores de bajo valor, tales como dos de 10 Ω en paralelo, como sustituto del fusible. Esto sólo ofrece una protección muy limitada en caso de cortocircuito: la corriente con los dos resistores de 10 Ω en paralelo sería de 1 A y la potencia disipada de 5 W, la mitad en cada uno de los resistores y diez veces lo que un resistor de 250 mW (comunes y baratos) está diseñado para soportar.
- Hay, por otro lado, información con mejor aspecto que indica que, de acuerdo con las bandas de colores del fusible, éste sería uno rápido de 390 mA.
Medí la intensidad consumida por un mando en reposo con dos dispositivos de memoria conectados. Salió algo entre 70 mA y 80 mA. Supongamos una intensidad característica de 80 mA. La Dreamcast tiene cuatro puertos de entrada para mandos, lo que daría una intensidad de 320 mA. Un fusible de 390 mA no parece descabellado.
Volvamos a la solución de los dos resistores de 10 Ω conectados en paralelo. Si los mandos fueran consumidores de corriente muy rígidos, una resistencia de 5 Ω daría una caída de tensión de 1,6 V y cada uno de los resistores disiparía en torno a sus 250 mW; en la práctica, los mandos consumirían menos corriente al ver menos tensión de alimentación e incluso funcionarían mal.
Categorías: Electricidad
Patillaje de los puertos de entrada de la Sega Dreamcast
2012-08-08
Reparé una videoconsola Sega Dreamcast hace unos días. Encontré alguna información sobre el patillaje de los mandos. Esta información, limitada a la clavija del mando (no trata el enchufe correspondiente de la videoconsola), está muy bien, pero puede conducir a algún error. La patilla 4 está marcada como sense en el artículo enlazado y está conectada a tierra en el mando. Cualquiera diría que, con ese nombre, la patilla estaría conectada a una entrada digital (con pull-up a alimentación) en la videoconsola, pero no es el caso. La siguiente imagen muestra el patillaje del lado videoconsola.
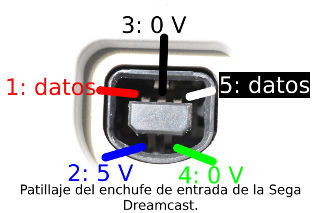
Patillaje de uno de los cuatro puertos de entrada (donde van
enchufados los mandos) de la Sega Dreamcast.
La patilla 4 está peligrosamente cerca de la patilla 2. La última lleva la alimentación a 5 V y la primera resulta que está conectada a tierra no sólo en el mando, sino también en la videoconsola. Pasan cosas feas si ambas patillas se tocan cuando la máquina está encendida.
La página enlazada está muy bien y contiene muchos datos francamente interesantes. La página principal es ésta: Dreamcast Programming. La elaboró un tal Marcus Comstedt (a gentleman and a scholar, I must say!).

La videoconsola en cuestión con un mando enchufado.
Categorías: Electricidad
Permalink: https://sgcg.es/articulos/2012/08/08/patillaje-de-los-puertos-de-entrada-de-la-sega-dreamcast/
Fabricación aditiva («impresión 3D») y armas: ya tenemos un nuevo demonio para vender periódicos
2012-08-04
Recientemente, una persona montó un arma de fuego con piezas comerciales y con piezas que hizo con una máquina de fabricación aditiva con control numérico (una «impresora 3D»). Esto, que no es en absoluto extraordinario (la gente lleva toda la vida fabricando armas en pequeños talleres domésticos), ha generado suficiente polémica para llamar la atención de la prensa. El 26 de junio salió un articulillo sobre este asunto en Popular Science y la cosa llegó el miércoles a un diario español, según me informó D.G.
Hay varias cosas que decir. La primera, que el individuo que es el centro de la polémica no fabricó el arma completa, sino sólo la caja (la caja inferior, pues el arma en cuestión, el rifle AR-15, tiene la caja dividida en dos). Esto es más o menos equivalente a fabricar el cuadro de una bicicleta frente a fabricar una bicicleta completa. Ahora bien, de acuerdo con la regulación estadounidense, la caja es el arma objeto de control legal específico y todo lo demás es un montón de accesorios. Otras piezas, tales como el mecanismo de disparo, van aparte. La regulación estadounidense, en cualquier caso, está más bien extendida a la venta de armas; no hace falta registrar la caja de un arma hecha en casa si ésta es sólo para uso personal. La pieza problemática es ésta. El proceso de montar el arma está documentado en dos artículos del propio individuo: uno y dos.
El articulillo de Popular Science termina con una patraña. Dice que cualquiera podrá usar una «impresora 3D» (es decir, una máquina de fabricación aditiva con control numérico) para hacer armas. Pues vale, pues me alegro. En Estados Unidos no hay precisamente escasez de armas de fuego hechas en pequeños talleres domésticos con tornos y fresadoras de guiado manual. Las armas de fabricación casera no son novedosas. Despejen el camino. No hay nada que ver aquí.
Categorías: Actualidad, DIY
