Tensiones o esfuerzos mecánicos (7)
2015-08-21
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. La fuerza por unidad de superficie medida resulta de aplicar este tensor sobre la dirección perpendicular a la superficie de medida y, en general, no es paralela a dicha dirección. Ahora bien, hay ciertos planos para los que la tensión medida sí es paralela a la dirección perpendicular. Las tensiones correspondientes son las tensiones principales y las direcciones de medida son las direcciones principales.
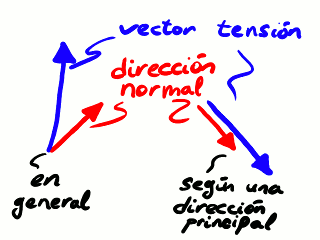
Concepto de dirección principal y tensión principal.
Tensiones principales
El vector tensión t medido en la dirección normal n cuando el tensor de tensiones es σ sale de la siguiente relación:
t = σ ⋅ n.
En general, el vector tensión y el vector normal no son necesariamente paralelos. Ahora bien, hay algunas direcciones (las direcciones principales) para las que sí se cumple que los vectores tensión salen paralelos a ellas. Podemos escribir la condición de paralelismo de la siguiente manera:
t = λ n = σ ⋅ n.
La constante de proporcionalidad λ es la tensión principal correspondiente a la dirección principal. En notación de componentes, tenemos las siguientes ecuaciones en las que es importante el uso de la simetría del tensor de tensiones.
σ11 n1 + σ12 n2 + σ13 n3 = λ n1;
σ12 n1 + σ22 n2 + σ23 n3 = λ n2;
σ13 n1 + σ23 n2 + σ33 n3 = λ n3.
En estas tres ecuaciones, tanto las componentes n1, n2 y n3 de la dirección principal como la tensión principal λ son incógnitas. Se trata de un problema autovalores convencional que puede tener hasta 3 soluciones linealmente independientes. Las direcciones principales son ortogonales entre sí. Para comprobarlo, tomemos 2 direcciones principales representadas por las matrices columna n1 y n2 (no hay que confundirlas con la notación de componentes de antes) que llevan sus componentes en coordenadas cartesianas. Las tensiones principales correspondientes son λ1 y λ2. El tensor tensión está representado por la matriz simétrica σ con sus componentes en coordenadas cartesianas. Tenemos las siguientes relaciones:
(σ−λ1) n1 = 0;
(σ−λ2) n2 = 0.
Si premultiplicamos la primera por (n2)T (la traspuesta de n2) y la segunda ecuación por (n1)T (la traspuesta de n1), queda lo siguiente:
(n2)T (σ−λ1) n1 = 0;
(n1)T (σ−λ2) n2 = 0.
Tomemos la traspuesta de la segunda ecuación. Gracias a la simetría de la matriz de tensiones, queda así:
(n2)T (σ−λ2) n1 = 0.
Restemos la primera ecuación y esta traspuesta de la segunda ecuación:
(n2)T [(σ−λ1) − (σ−λ2)] n1 = (λ1−λ2) (n2)T n1 = 0.
Si las tensiones principales escogidas son diferentes, el producto de las direcciones principales es nulo, lo que implica que son perpendiculares. Si varias tensiones principales son iguales, entonces las direcciones principales no están completamente definidas, ya que es posible rotarlas arbitrariamente dentro del espacio en el que se mueven.
Digamos que tenemos tres soluciones de la incógnita λ del polinomio característico: σ1, σ2 y σ3. Se trata de las tensiones principales. En un sistema de referencia cuyos ejes coordenados son las direcciones principales, la matriz de tensiones que representa al tensor de tensiones en tal eje es diagonal y tiene la siguiente forma:
| σ1 | 0 | 0 |
| 0 | σ2 | 0 |
| 0 | 0 | σ3 |
En ejes principales, no hay tensiones tangenciales o cortantes.
La transformación de un sistema de coordenadas al otro se hace mediante una transformación de semejanza normal y corriente. Si σ es la matriz de tensiones en la base original, σ' es la matriz de diagonal en la base de los ejes principales y N es la matriz con los autovectores normalizados (una matriz cuyas columnas son las componentes de las direcciones principales, cada columna con norma euclídea unidad), el cambio de base se realiza así:
σ' = C−1 σ C.
Ahora bien, como los ejes principales son ortonormales, la matriz de cambio de base es ortogonal y la expresión es todavía más sencilla, ya que la inversión se reduce a una trasposición:
σ' = CT σ C.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/21/tensiones-o-esfuerzos-mecanicos-7/
