Haber crecido de forma exponencial
2016-10-12
A menudo, al describir un aumento grande de alguna magnitud durante
un intervalo de tiempo dado, se dice que tal magnitud ha crecido de
forma exponencial
. Esta expresión, lamentablemente, suele estar
mal empleada en estos casos, ya que la naturaleza exponencial de un
crecimiento indica un comportamiento sostenido en el tiempo, no una
comparación entre dos estados puntuales: no tiene sentido hablar de un
crecimiento exponencial entre un resultado al cierre de un año y el
mismo resultado al cierre del año siguiente, por ejemplo. Es la
naturaleza dinámica (de cierto tipo específico) prolongada a lo largo
de cierto intervalo lo que hace que un crecimiento sea exponencial
durante dicho intervalo, no el hecho de que un crecimiento puntual,
aislado, haya sido grande. En concreto, para que una magnitud crezca
de forma exponencial, su tasa de variación ha de ser proporcional a su
valor instantáneo de forma sostenida.
Naturaleza matemática del crecimiento exponencial
Una magnitud varía de forma exponencial cuando el ritmo al que varía es proporcional a su propio valor. Si la magnitud depende de de forma continua del tiempo t como x(t), su ritmo de variación ha de quedar modelado satisfactoriamente de la forma siguiente para que su comportamiento sea exponencial:
(d⁄dt)x(t) = k x(t).
En la anterior ecuación, k es una constante de proporcionalidad que, además, ha de ser positiva si la magnitud ha de crecer. Si, por el contrario, la magnitud está dada en instantes discretos de tiempo equiespaciados t0, t1, t2, … tn, …, su variación ha de quedar bien aproximada de la siguiente forma:
x(tn+1) − x(tn) = k x(tn).
Igual que antes, la constante k ha de ser positiva para que la magnitud crezca.
En ambos casos, se habla de crecimiento exponencial porque la ley que cumple que su tasa de variación es proporcional a su magnitud instantánea es exponencial. En el caso continuo, si conocemos el valor en un instante dado t0, la magnitud depende del tiempo explícitamente de la siguiente manera:
x(t) = x(t0) ek (t−t0).
En el caso discreto, la ley es la siguiente:
x(tn) = x(t0) (k+1)n.
Sucede que la ley exponencial, cuando la constante de proporcionalidad k es positiva, el valor de la magnitud se hace tan grande como se quiera (y su tasa de variación también lo hace) sin más que escoger un tiempo lo bastante grande: el crecimiento exponencial es muy rápido si se le deja el suficiente tiempo.
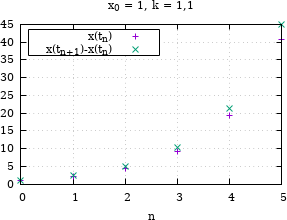
Ejemplo de crecimiento exponencial.
Categorías: Lingüística, Matemáticas
Permalink: https://sgcg.es/articulos/2016/10/12/haber-crecido-de-forma-exponencial/
