Diseño de un carrito para guardar unas pesas (2)
2017-01-10
Tengo un hueco estrecho, que he decidido aprovechar con un carrito para guardar unas pesas. Las pesas tienen una masa conjunta que no supera los 60 kg, así que, como mucho, el carrito soportará de forma estática una carga de unos 600 N repartida por toda su estructura. La carga, no obstante, puede hacerse algo mayor al guardar las pesas y al mover el carrito. Hoy toca dimensionar la estructura. Para hacer un diseño seguro, supondremos una carga superior (de 1 kN) aplicada únicamente en el centro de una de las baldas.
Baldas
Por cuestiones de disponibilidad, precio, facilidad de mecanizado y presentación, encuentro interesante hacer las baldas (y el resto del esqueleto de estantería del carrito) a partir de tableros de aglomerado con un chapado similar al de los muebles colindantes. Todas las dimensiones de los tableros, salvo el espesor, están dadas por los criterios funcionales y geométricos explicados en el artículo anterior. Falta decidir el espesor, que puede ser de 10 mm o de 16 mm. Echemos unas cuentas.
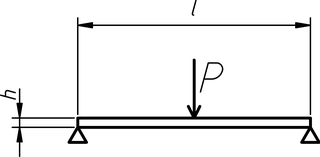
Modelo del estado de carga de la balda como una viga simplemente
apoyada. La tensión máxima se da en la en las fibras extremas de la
sección central.
Una balda de espesor h, ancho b y longitud l simplemente apoyada en sus extremos y sometida a una carga P en su sección central experimenta una tensión máxima
σ = (3 ⁄ 2) (P l) ⁄ (b h2).
Con una carga de 1 kN (correspondiente a una masa de unos 100 kg, que es casi el doble del total que tiene que soportar el carrito), una balda de 16 mm de espesor, 17 cm de ancho y 40 cm de longitud experimenta una tensión máxima de 14 MPa, que es algo muy próximo a la resistencia a la flexión típica de tablero de aglomerado. Los tableros de 10 mm de espesor son demasiado débiles incluso para una carga de 500 N, así que la elección es clara: hay que usar tableros de 16 mm de espesor. Estos tableros valen tanto para las baldas como para los paneles verticales laterales.
Este dimensionado da un factor de seguridad muy generoso. El carrito nunca va a encontrarse con una carga concentrada de 1 kN en el centro de cada balda, sino que se limitará a quizá 600 N en total repartidos en su mayoría a lo largo de la balda inferior y la balda central.
Uniones entre tableros

Espigas.
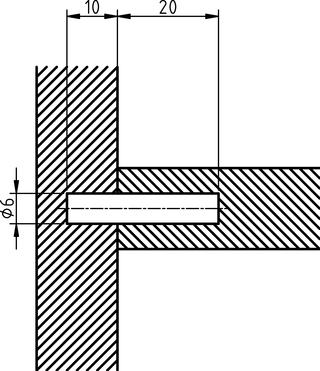
Esquema de la unión mediante espigas.
Las baldas han de estar unidas a los paneles verticales de alguna manera. Una opción muy cómoda es usar espigas de madera. Las hay de haya de varias dimensiones. Para mantener una balda fija, basta poner dos espigas en un extremo y dos espigas en el otro. Las más pequeñas que había disponibles eran de 6 mm de diámetro y 30 mm de longitud. Con taladros de 10 mm de profundidad en los paneles verticales y 20 mm de profundidad en las baldas, la parte más débil de la unión está en los paneles verticales. Estimemos la solicitación bajo las siguientes hipótesis, que modelan aproximadamente el estado justo antes de que la estructura se venga abajo:
- la carga (digamos, como antes, 1 kN) se reparte uniformemente entre las cuatro espigas;
- el contrachapado del panel vertical soporta en cada unión una compresión igual a la carga transmitida por la espiga correspondiente (un cuarto de la total) dividida entre la superficie en planta de la unión (10 mm por 6 mm).
Con estas hipótesis, sale una compresión de unos 4 MPa en las uniones con los paneles verticales. La resistencia a la compresión de un panel de aglomerado puede rondar los 15 MPa y la carga elegida es mucho mayor que la real, así que puede considerarse que la estructura aguantará.
Puede hacerse un cálculo similar al anterior para la unión con las baldas. Resulta también que la unión aguanta. El problema en este caso no es de compresión: la tensión tiende a astillar el aglomerado.
Finalmente, está la posibilidad de que las espigas fallen a cortadura. La carga de la espiga queda repartida uniformemente en su sección transversal de 6 mm de diámetro, lo que da unos 9 MPa con la carga sobreestimada de diseño. La resistencia a la cortadura (perpendicular a la fibra) del haya es mucho mayor.
Ruedas
Esta parte del diseño es la más inmediata. El catálogo de ruedas ya indica su resistencia. Hay ruedas fijas (que no pivotan) de 25 mm de diámetro que pueden soportar una masa de 25 kg sobre ellas. Con cuatro ruedas, el carrito puede soportar una masa de 100 kg, lo que corresponde a una fuerza de 1 kN.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2017/01/10/diseno-de-un-carrito-para-guardar-unas-pesas-2/
