La distribución log-normal y los salarios
2017-02-25
La distribución de los salarios (es decir, la proporción de trabajadores por rangos de salario) suele quedar bien modelada mediante una distribución log-normal, quizá con una cola que sigue una distribución de Pareto para el 3 % o el 1 % que más gana. Como ilustración del concepto, en este artículo hacemos una comparación visual rápida de los salarios españoles y el modelo log-normal aplicado a ellos.
Distribución log-normal
Según la distribución log-normal, el salario S de un individuo cualquiera tiene una probabilidad de ser igual o inferior a un nivel salarial s que puede expresarse mediante la siguiente expresión:
E[S<s] = (1 ⁄ 2) + (1 ⁄ 2) erf{[ln(s) − μ] ⁄ [σ √2]}.
El parámetro σ es positivo y viene a gobernar la escala de la distribución. El parámetro μ tiene un valor real en general y viene a gobernar la posición de la distribución.
La densidad de probabilidad, que es la probabilidad de que el salario S de un individuo cualquiera se encuentre en el intervalo infinitesimal entre el nivel s y s+ds, es la siguiente:
E[s<S<s+ds] = {1 ⁄ [s σ √(2π)]} e−[ln(s)−μ]2 ⁄ [2 σ2].
El salario medio es
E[S] = eμ + σ2 ⁄ 2.
El salario mediano es
eμ.
El salario moda es
eμ −σ2.
La varianza es
E[S2] − (E[S])2 = (eσ2 − 1) e2μ2 +σ2.
Ajuste a los salarios españoles de 2014
Es fácil verificar el modelo de distribución log-normal en España con los datos publicados por el Instituto Nacional de Estadística. Como ilustración, usé los resultados de la encuesta de estructura salarial de 2014 para trabajadores a tiempo completo, que vienen desglosados entre hombres y mujeres y en tramos que abarcan múltiplos enteros del salario mínimo interprofesional: de 0 a 1, de 1 a 2, de 2 a 3, de 3 a 4, de 4 a 5, de 5 a 6, de 6 a 7, de 7 a 8, y salarios superiores. Hice unos sencillos ajuste de mínimos cuadrados exceptuando los salarios superiores a 8 veces el salario mínimo interprofesional, ya que estos últimos tramos ocupan los percentiles que quedan mejor modelados mediante una distribución de Pareto. La calidad del ajuste no cambia apreciablemente, no obstante. Con datos de salario expresados en unidades del salario mínimo interprofesional, los parámetros que mejor cuadran el modelo con los resultados son:
- μ ≈ 0,91 y σ ≈ 0,47 para los totales;
- μ ≈ 0,84 y σ ≈ 0,46 para las mujeres;
- μ ≈ 0,95 y σ ≈ 0,47 para los hombres.
Los parámetros de escala son casi los mismos, pero hay una diferencia en el factor de posición. Según el modelo log-normal:
- el salario medio es 2,8, el salario mediano es 2,5, el salario moda es 2,0 y la varianza es 1,9 para los parámetros ajustados a los datos totales;
- el salario medio es 2,6, el salario mediano es 2,3, el salario moda es 1,9 y la varianza es 1,6 para los parámetros ajustados a los datos de las mujeres;
- el salario medio es 2,9, el salario mediano es 2,6, el salario moda es 2,1 y la varianza es 2,1 para los parámetros ajustados a los datos de los hombres.
Siguen las gráficas de los modelos en comparación con los datos del Instituto Nacional de Estadística:
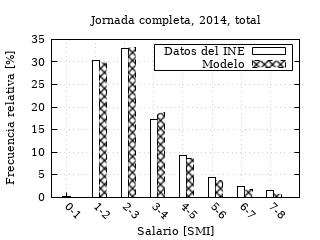
Datos del INE frente al modelo log-normal para todos los
trabajadores españoles a jornada completa en 2014.

Datos del INE frente al modelo log-normal para las mujeres
trabajadoras españolas a jornada completa en 2014.

Datos del INE frente al modelo log-normal para los hombres
trabajadores españoles a jornada completa en 2014.
La siguiente gráfica muestra una comparación de las densidades de probabilidad totales, de mujeres y de hombres:
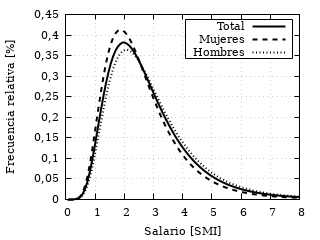
Modelos log-normales de salarios españoles para jornada completa
en 2014.
Categorías: Matemáticas
Permalink: https://sgcg.es/articulos/2017/02/25/la-distribucion-log-normal-y-los-salarios/
