Presión de la radiación isótropa
2014-08-26
Es posible deducir la ley de Stefan-Boltzmann mediante un razonamiento termodinámico macroscópico muy sencillo. Para poder realizar este razonamiento, primero necesitamos deducir la presión de la radiación isótropa. Deduciremos que la presión de la radiación es igual a la tercera parte de la densidad de energía.
Nos centramos alrededor de un determinado punto y fijamos un área infinitesimal dA. Definimos un sistema de coordenadas esféricas centrado en nuestro punto de estudio como en la figura:
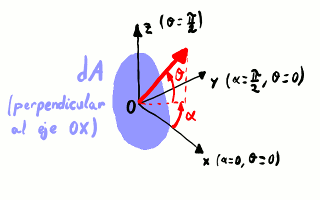
Sistema de coordenadas esféricas. Si miramos en una dirección
dada desde el punto bajo estudio, la elevación es el
ángulo θ y el acimut es el
ángulo α. La superficie
infinitesimal dA es perpendicular a
la dirección θ = 0, α =
0.
La radiación es isótropa, así que viene con la intensidad I (una potencia por unidad de superficie) de todas direcciones por igual. La energía contenida en un volumen
La radiación, isótropa, es igual a la superposición de frentes de onda de intensidad I que viajan en todas direcciones con rapidez c (la de la luz). Esta intensidad es un flujo de potencia por unidad de superficie y el flujo de potencia por unidad de superficie es lo mismo que la densidad u de energía por unidad de volumen multiplicada por la rapidez c con la que se propaga esta energía. Ya explicamos por qué era esto así en el artículo del teorema del transporte de Reynolds. La densidad de energía en un punto dado es igual a la resultante de la de todas las direcciones:
u = ∫dα∫θcos(θ) dθ I ⁄ c = 4 π I ⁄ c,
con el intervalo de integración definido de α = −π a α = π y de θ = −π ⁄ 2 a θ = π ⁄ 2.
La radiación electromagnética transporta cantidad de movimiento. La cantidad de movimiento de un fotón es igual a su energía dividida por la rapidez de la luz. Por lo tanto, la densidad p de cantidad de movimiento por unidad de volumen de un frente de onda es igual a
I ⁄ c2.
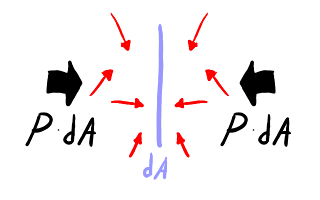
Equilibrio de fuerzas sobre la superficie elemental. La presión
ejercida por la radiación en una cara se contrarresta por la presión
ejercida por la radiación en la cara opuesta.
Hagamos como que la superficie dA es sólida. Como la radiación es isótropa, la superficie suporta una fuerza por un lado y la fuerza opuesta por el otro, de manera que la fuerza total es nula. La fuerza ejercida a un lado está relacionada con la presión P: es igual a P dA. Por otra parte, la fuerza se debe a la cantidad de movimiento que impacta y rebota por un lado de la superficie: es igual al doble de la cantidad de movimiento normal incidente. La componente tangencial no afecta a la cantidad de movimiento. La componente normal a la superficie dA de un frente de onda dirigido con acimut α y elevación θ es
(I ⁄ c2) ⋅ cos(α) ⋅ cos(θ).
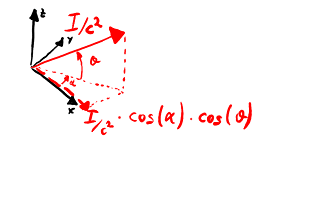
Densidad de cantidad de movimiento de un rayo y su componente
normal a la superficie (es decir, su proyección sobre el
eje OX: α =
0, θ = 0).
Esta cantidad de movimiento normal es transportada con velocidad normal
c ⋅ cos(α) ⋅ cos(θ).
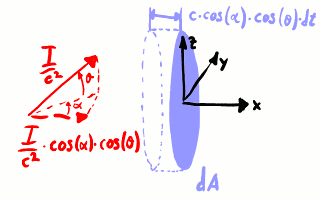
Transporte de la cantidad de movimiento normal de un rayo. Tras
un tiempo dt, ha incidido sobre la
superficie dA la cantidad de
movimiento normal contenida en el
volumen dA c cos(α) cos(θ) dt:
una cantidad de movimiento igual
a [(I ⁄ c2) cos(α) cos(θ)] [dA c cos(α) cos(θ) dt].
Esta cantidad de movimiento dividida por el intervalo de
tiempo dt es la cantidad de
movimiento normal de un rayo transportada perpendicularmente a la
superficie por unidad de tiempo.
La fuerza total en una de las caras de la superficie dA es igual al doble del resultado de la cantidad de movimiento normal transportada a la velocidad normal incidente desde esa cara de la superficie:
P dA = 2 dA ∫dα∫cos(θ) dθ [(I ⁄ c2) cos(α) cos(θ)] [c cos(α) cos(θ)] = (4 ⁄ 3) π dA I ⁄ c,
con el intervalo de integración definido de α = −π a α = π y de θ = −π ⁄ 2 a θ = π ⁄ 2. Por lo tanto, la presión es un tercio de la densidad de energía:
P = (4 ⁄ 3) π I ⁄ c = u ⁄ 3.
Este resultado es lo que buscábamos.
Categorías: Física
