Ecuación del calor
2014-08-31
La ecuación del calor es una de las ecuaciones más famosas de la física matemática. Es la base para modelar la evolución de ciertos fenómenos difusivos como la transmisión de calor por conducción.
Hipótesis
Tenemos un medio:
- continuo;
- homogéneo;
- isótropo;
- estático (ni se desplaza ni cambia de forma);
- en equilibrio termodinámico local;
- en el que lo único que puede variar es la temperatura;
- en el que el único fenómeno que rige la transferencia de calor es la conducción;
- en el que el flujo de calor por conducción queda bien descrito mediante la ley de Fourier;
- en el que la energía térmica es directamente proporcional a la temperatura.
En lo que sigue, usaremos un sistema de referencia ligado al material. Como el medio se encuentra estático, la descripción lagrangiana y la descripción euleriana son idénticas.
Forma integral de la ecuación del calor
Asumimos que la densidad de energía interna u en un punto del cuerpo de densidad ρ a temperatura T es
u ≡ ρ c T.
La constante c es el calor específico del material (su capacidad calorífica por unidad de masa a volumen constante).
Cuando hay un gradiente ∇T de temperatura en un punto dado, se produce un flujo de calor q de acuerdo con la ley de Fourier:
q ≡ −k ∇T.
Si nos centramos en un volumen cualquiera V del cuerpo, vemos que su energía interna puede variar con el tiempo t:
(d⁄dt)∫∫∫Vu dV = ∫∫∫Vρ c dT ⁄ dt dV.
Esta variación se debe a algo. En virtud del primer principio de la termodinámica, esta variación con el paso del tiempo ha de deberse al flujo de calor que atraviesa perpendicular la superficie de frontera S del volumen:
(d⁄dt)∫∫∫Vu dV = ∫∫S−q ⋅ n dS = ∫∫Sk ∇T ⋅ n dS.
El símbolo n indica el vector normal a la superficie de frontera que apunta hacia el exterior. Como la normal apunta hacia el exterior, el flujo es positivo cuando sale energía del volumen, con lo que el efecto va con el signo opuesto. Si unimos las dos ecuaciones, nos queda una en función de la temperatura:
∫∫∫Vρ c ∂T ⁄ ∂t dV = ∫∫Sk ∇T ⋅ n dS.
Esta ecuación es una forma de expresar la ecuación del calor y se aplica a volúmenes cualquiera del cuerpo.
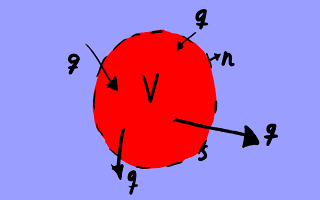
Flujo de calor a través de la
frontera S de un
volumen V. El
flujo q, que es vectorial,
solamente afecta en su componente según la dirección normal local
n.
Forma diferencial de la ecuación del calor
Partimos de la forma integral y aplicamos el teorema de la divergencia para que todas las integrales sean volumétricas:
∫∫∫Vρ c ∂T ⁄ ∂t dV = ∫∫∫Vk ∇2T dV.
El operador ∇2 es la laplaciana.
Podemos reagrupar los términos a la izquierda del signo de la igualdad:
∫∫∫V(ρ c ∂T ⁄ ∂t − k ∇2T) dV = 0.
Como esto se aplica a cualquier volumen de integración dentro del cuerpo, el integrando ha de ser exactamente nulo siempre:
ρ c dT ⁄ dt − k ∇2T = 0.
Podemos reunir todas las constantes en una a la que llamaremos α:
∂T ⁄ ∂t − α ∇2T = 0.
Esta ecuación es la forma diferencial de la ecuación del calor. Hay que complementarla con condiciones iniciales (la distribución de temperatura en un instante inicial) y condiciones de contorno (la temperatura o el flujo de calor en el contorno). Generalizar la ecuación del calor a otro número de dimensiones espaciales es elemental: solamente hay que usar la laplaciana ∇2 correspondiente.
Algunas propiedades de la ecuación del calor
La ecuación del calor es una ecuación parabólica. El calor se transmite al instante a cualquier distancia, pero los efectos solamente son grandes a distancias cortas y se aproximan a ser nulos a distancias grandes.
La ecuación del calor es muy agradecida. Tiende a alisar las irregularidades de las condiciones iniciales hasta alcanzar un estado estacionario que es independiente de la situación de partida; esto facilita el cálculo de soluciones aproximadas.
El problema de evolución hacia atrás en el tiempo está mal condicionado. En vez de suavizarse, las irregularidades se acentúan hacia atrás en el tiempo.
Categorías: Física
Permalink: http://sgcg.es/articulos/2014/08/31/ecuacion-del-calor/
