Tensiones o esfuerzos mecánicos (12)
2015-09-12
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hay varias maneras de resumir las características de este tensor; algunas, como el elipsoide de Lamé, son representaciones geométricas. El artículo de hoy trata sobre los círculos de Mohr, que son otra representación geométrica que además permite el cálculo gráfico de la componente normal y la componente tangencial del vector tensión.
Los círculos de Mohr
Los círculos de Mohr son una representación de los posibles valores que pueden adoptar la tensión normal y la tensión cortante al variar la dirección de medida.
Trabajemos en ejes principales con la numeración escogida tal que las tensiones principales están ordenadas de la siguiente manera:
σ1 ≥ σ2 ≥ σ3.
Medido en una dirección cualquiera (actuando sobre un plano cualquiera) dada por el vector normal n, el vector tensión t tiene componentes
ti = σi ni, i ∈ {1,2,3}.
El cuadrado del módulo de este vector tensión es
t ⋅ t = (σ1)2 (n1)2 + (σ2)2 (n2)2 + (σ3)2 (n3)2.
El vector normal se descompone en una componente normal al plano de medida (paralela a la dirección de medida) de magnitud σ (la tensión normal) y una componente tangente al plano de medida (perpendicular a la dirección de medida) de magnitud τ (la tensión tangencial). La tensión normal sale, por lo tanto, de proyectar sobre el vector normal:
σ ≡ t ⋅ n = σ1 (n1)2 + σ2 (n2)2 + σ3 (n3)2.
La magnitud del vector tensión está relacionada con la tensión normal y la tensión tangencial mediante el Pitágoras:
t ⋅ t = σ2 + τ2.
Tanto esta ecuación del teorema de Pitágoras como la primera del cuadrado del módulo del vector tensión son lineales en los cuadrados de las componentes del vector normal. Otra ecuación con la misma forma es la que establece que el vector normal tiene, por definición, módulo unitario:
(n1)2 + (n2)2 + (n3)2 = 1.
Asumamos ahora que las tensiones principales son diferentes entre sí. El sistema de tres ecuaciones queda diagonalizado de la siguiente manera:
(σ1−σ2) (σ1−σ3) (n1)2 = (σ−σ2) (σ−σ3) + τ2;
(σ2−σ1) (σ2−σ3) (n2)2 = (σ−σ3) (σ−σ1) + τ2;
(σ3−σ1) (σ3−σ2) (n3)2 = (σ−σ1) (σ−σ2) + τ2.
Estas ecuaciones se prestan a una interpretación geométrica muy interesante en el plano (σ,τ). Hay varias conclusiones que podemos extraer: por una parte, las tensiones normales y tangenciales ocupan el lugar geométrico interior a una circunferencia grande y exterior a dos circunferencias pequeñas (los círculos de Mohr); por otra parte, es posible usar las propiedades de la potencia de un punto respecto a una circunferencia para determinar gráficamente la tensión normal y la tensión tangencial en una dirección cualquiera.
Lugar geométrico de las tensiones
Debido al orden de las tensiones principales y a que los cuadrados de las componentes de la dirección normal son positivos, salen las siguientes inecuaciones que fijan el lugar geométrico de las tensiones normales y tangenciales:
(σ−σ2) (σ−σ3) + τ2 ≥ 0;
(σ−σ3) (σ−σ1) + τ2 ≤ 0;
(σ−σ1) (σ−σ2) + τ2 ≥ 0.
Estas tres inecuaciones determinan los siguientes lugares geométricos:
- El exterior de un círculo centrado en el punto σ = (σ3+σ2) ⁄ 2, τ = 0 y de radio σ2−σ3 (un círculo de radio pequeño).
- El interior de un círculo centrado en el punto σ = (σ3+σ1) ⁄ 2, τ = 0 y de radio σ1−σ3 (un círculo de radio grande).
- El exterior de un círculo centrado en el punto σ = (σ1+σ2) ⁄ 2, τ = 0 y de radio σ1−σ2 (un círculo de radio pequeño).
Estos círculos son los círculos de Mohr. Los puntos en el plano de las tensiones se encuentran en la región que es a la vez interior al círculo grande y exterior a los círculos pequeños.
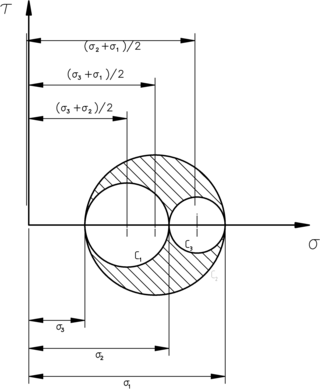
Círculos de Mohr. Las tensiones pueden adoptar valores en el área
rayada.
Cálculo gráfico de las tensiones
El sistema de ecuaciones diagonalizado es, además, el de la potencia de un punto con respecto a los círculos (las circunferencias) de Mohr. En concreto, el lado derecho de cada ecuación es la potencia respecto a la circunferencia correspondiente. El lado izquierdo de cada ecuación está en forma de producto de dos diferencias y el cuadrado de un coseno director, análogo al producto de dos distancias que es la potencia de un punto respecto a una circunferencia. Basta construir estas distancias. Las siguientes figuras muestran construcciones que cumplen las respectivas ecuaciones de la potencia:
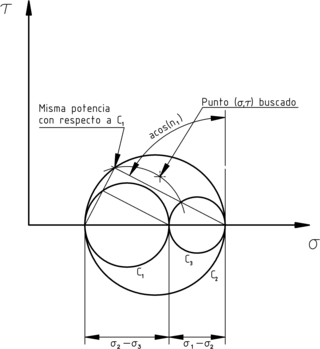
Potencia relativa a la circunferencia 1.
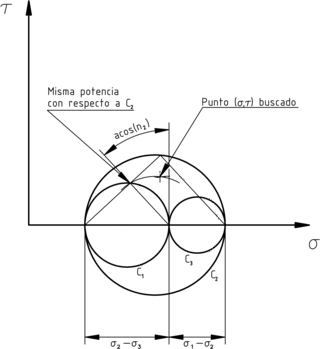
Potencia relativa a la circunferencia 2. También puede hacerse la
construcción análoga en sentido horario.
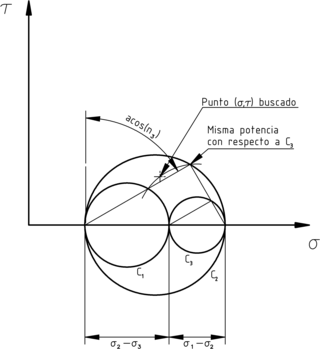
Potencia relativa a la circunferencia 3.
Basta usar 2 de estas construcciones para calcular gráficamente la tensión normal y la tensión tangencial cuando se conocen las componentes del vector normal:
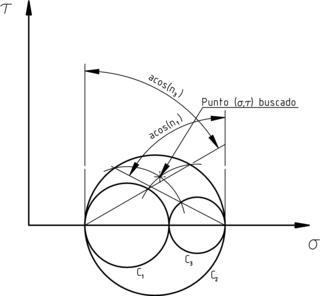
Cálculo gráfico de la descomposición del vector tensión. En cada
punto σ
= σi, τ = 0 se traza
una línea desviada de la vertical el
ángulo acos(ni) y
seguidamente se traza un arco concéntrico con la
circunferencia Ci que
corte la intersección de la línea con las otras circunferencias. El
punto buscado es la intersección de los arcos trazados.
El mismo principio permite calcular gráficamente las direcciones normales correspondientes a un punto en el plano (σ,τ).
Máxima tensión tangencial
De la construcción de los círculos de Mohr se deduce que la máxima tensión tangencial o cortante es igual al radio del círculo mayor:
τmáx = σ1−σ4.
Del cálculo gráfico se deduce que las componentes del vector normal son
n1,τmáx = cos(π ⁄ 4) = (√2) ⁄ 2;
n2,τmáx = cos(π ⁄ 2) = 0;
n3,τmáx = cos(π ⁄ 4) = (√2) ⁄ 2.
Tensiones principales iguales
Cuando las 3 tensiones principales son iguales, los círculos de Mohr colapsan en un punto. Es un estado de tensión hidrostática pura.
Cuando σ1 = σ2 ≠ σ3, el lugar geométrico de las tensiones se limita a la circunferencia mayor C2.
Cuando σ3 = σ2 ≠ σ1, el lugar geométrico de las tensiones es el interior completo de la circunferencia mayor C2.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/09/12/tensiones-o-esfuerzos-mecanicos-12/
