Tensiones o esfuerzos mecánicos (13)
2016-06-06
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos hace unos meses que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hay varias maneras de resumir las características de este tensor; algunas, como el elipsoide de Lamé, son representaciones geométricas. Hoy vamos a estudiar otra de estas representaciones geométricas: la cuádrica indicatriz de tensiones.
La cuádrica indicatriz de tensiones
Para hacer los cálculos sencillos, vamos a trabajar en ejes principales. Las tensiones principales son
σ1 ≤ σ2 ≤ σ3.
De ahora en adelante, asumimos que al menos una de las tensiones principales es no nula; si todas fueran nulas, el estudio de las tensiones sería trivial.
En una dirección cualquiera caracterizada por el vector unitario n de componentes en ejes principales
{n1, n2, n3},
el vector tensión t tiene componentes
t1 = n1 σ1;
t2 = n1 σ2;
t3 = n1 σ3.
La tensión normal σ, que es la proyección del vector tensión t en la dirección de medida n, es
σ ≡ t ⋅ n = σ1 (n1)2 + σ2 (n2)2 + σ3 (n3)2.
Hasta aquí, todo es una repetición de lo que vimos en artículos anteriores. Ahora, tomemos un vector x de componentes
x1 ≡ n1 ⁄ √|σ|;
x2 ≡ n2 ⁄ √|σ|;
x3 ≡ n3 ⁄ √|σ|.
Al sustituir las componentes del vector normal n con las del nuevo vector x en la ecuación de la tensión normal, sale lo siguiente:
σ ⁄ |σ| = signo(σ) = σ1 (x1)2 + σ2 (x2)2 + σ3 (x3)2.
Esta ecuación indica que el vector x está restringido a una superficie cuádrica: la cuádrica indicatriz de tensiones. La teoría de las superficies cuádricas permite obtener información sobre las tensiones.
Todas las tensiones principales positivas
Si las tres tensiones principales son estrictamente positivas, la cuártica indicatriz de tensiones describe un elipsoide. Si el signo de la tensión normal σ fuera negativo, el elipsoide sería imaginario y, por extensión, el propio vector normal n. Tampoco es posible que el signo sea indefinido (o 0). Por el contrario, si el signo de la tensión normal es positivo, el elipsoide es real. Por lo tanto, si todas las tensiones principales son positivas, la tensión normal siempre ha de ser positiva, es decir, de tracción, sin importar la dirección del vector normal a la superficie en la que se mide la tensión. La ecuación del elipsoide es la siguiente:
|σ1| (x1)2 + |σ2| (x2)2 + |σ3| (x3)2 = 1.
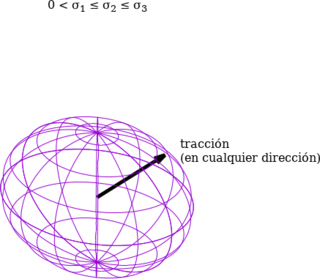
Cuádrica indicatriz de tensiones cuando todas las tensiones
principales son positivas.
Todas las tensiones principales negativas
Si las tres tensiones principales son estrictamente negativas, la cuártica indicatriz de tensiones describe un elipsoide con un comportamiento respecto al signo de la tensión normal opuesto al del caso de las tres tensiones principales estrictamente positivas. Por lo tanto, si las tres tensiones principales son estrictamente negativas, la tensión normal siempre es negativa, es decir, de compresión, sin importar la dirección del vector normal a la superficie en la que se mide la tensión. La ecuación del elipsoide es igual que antes:
|σ1| (x1)2 + |σ2| (x2)2 + |σ3| (x3)2 = 1.
Una tensión principal con un signo y las otras dos con el signo opuesto
Asumamos que σ3 > 0 y σ1 ≤ σ2 < 0. Como pasaba cuando todas las tensiones principales tenían el mismo signo, pasar al otro caso (σ1 < 0 y σ3 ≥ σ2 > 0) meramente consiste en un cambio de signos. La cuádrica indicatriz describe un hiperboloide de dos hojas cuando el signo de la tensión normal es positivo, un hiperboloide de una hoja cuando el signo de la tensión normal es negativo, y un cono elíptico (la frontera entre los hiperboloides de dos hojas y los hiperboloides de una hoja) en el caso degenerado en el que el signo se anula. Con tensión normal positiva, el hiperboloide tiene la siguiente ecuación:
−|σ1| (x1)2 − |σ2| (x2)2 + |σ3| (x3)2 = 1.
Con tensión normal negativa, el hiperboloide queda así:
−|σ1| (x1)2 − |σ2| (x2)2 + |σ3| (x3)2 = −1.
El caso degenerado es así:
−|σ1| (x1)2 − |σ2| (x2)2 + |σ3| (x3)2 = 0.
Dado que el vector x no es más que el vector normal n multiplicado por un escalar, es posible comparar directamente la dirección del vector normal con las cuádricas para saber el signo de la tensión normal σ. Se aprecia que si la dirección normal queda contenida en el interior del cono, al escalarla solamente es posible interceptar los hiperboloides de dos hoja; por lo tanto, el signo de la tensión normal es positivo (la tensión normal es de tracción). Por el contrario, si la dirección normal queda contenida en el exterior del cono, al escalarla solamente es posible interceptar los hiperboloides de una hoja; por lo tanto, el signo de la tensión normal es negativo (la tensión normal es de compresión). En los casos en los que la dirección normal coincide con la superficie del cono, la tensión normal es nula.
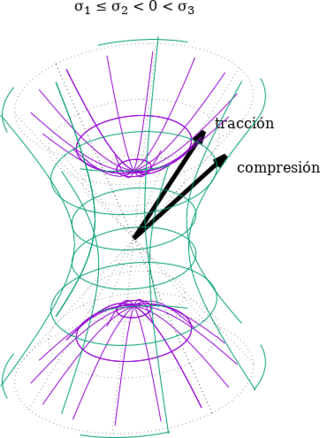
Cuádrica indicatriz de tensiones cuando dos tensiones principales
son negativas y la tercera es positiva. Las direcciones contenidas en
el interior del cono (marcado con puntos) tienen tensiones normales a
tracción y las direcciones contenidas en el exterior del cono tienen
tensiones normales a compresión.
Si los signos de las tensiones principales se invierten, los signos del análisis del párrafo anterior también lo hacen: con dirección normal en el interior del cono, la tensión normal es compresiva; con dirección normal en el exterior del cono, la tensión normal es de tracción.
Dos tensiones principales de signo idéntico y la otra nula
Este caso es como llevar al límite el del elipsoide o el del hiperboloide de una hoja: la cuártica degenera en un cilindro elíptico, tal que la tensión es siempre de tracción si las tensiones principales no nulas son positivas y es siempre de compresión si las tensiones principales no nulas son negativas. También puede prescindirse de la dimensión correspondiente a la tensión principal nula y analizar la cuádrica como una cónica (una elipse en este caso).

Cuádrica indicatriz de tensiones cuando dos tensiones principales
son de signo idéntico (en este caso, positivo) y la restante es nula.
Dos tensiones principales de signo opuesto y la otra nula
Este caso es una degeneración del caso de los hiperboloides y también puede verse como que las cuádricas degeneran en cónicas (hipérbolas) al eliminar la dimensión correspondiente a la tensión principal nula. El cono asintótico se transforma en dos rectas asintóticas que se cruzan en el origen y que dividen el plano en regiones alternantes entre compresión y tracción.
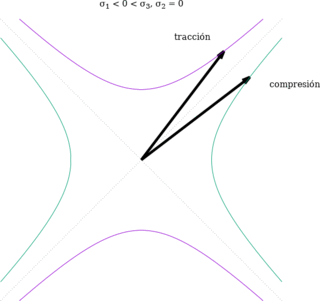
Cuádrica indicatriz de tensiones cuando dos tensiones principales
son de signo opuesto y la restante es nula.
Dos tensiones principales nulas y la otra no nula
En este caso, la cuártica es casi trivial y aporta escasa información útil. La tensión normal puede tener cualquier signo y se anula exactamente cuando la dirección normal al plano de medida es perpendicular a la dirección principal no nula.
Categorías: Física
Permalink: https://sgcg.es/articulos/2016/06/06/tensiones-o-esfuerzos-mecanicos-13/
