La botella y la bodega de avión (2)
2013-07-17
Introdujimos recientemente el problema de la supervivencia de una botella cerrada y llena de algún líquido en la bodega de un avión en vuelo. Vimos que aunque el avión está presurizado, la presión desciende un poco a gran altitud: puede bajar hasta unos 75 kPa, alrededor de 25 kPa menos que a nivel del mar y 20 kPa menos que en Madrid lejos de las montañas. Con la botella sellada, la presión interior no cambia significativamente porque la temperatura de la bodega no varía mucho, así que hay un exceso de presión Δp en el interior de la botella de esos 25 kPa si fue cerrada a nivel del mar. Este exceso de presión ha de estar dentro del rango que puede aguantar la botella sin perder su integridad.
Resistencia de la pared de la botella
Asumamos en primer lugar que el tapón aguanta en su sitio y mantiene la botella bien cerrada. Si es así, tendremos que ver si la propia botella es capaz de aguantar el esfuerzo debido a la diferencia de presión. La botella en sí es una estructura de pared delgada y podemos hacer algunas hipótesis simplificadoras que nos facilitan mucho los cálculos: las tensiones son muy aproximadamente uniformes según el espesor de la pared y la componente contenida en la superficie media de la pared es mucho mayor que cualquier otra. La siguiente figura ilustra lo que pasa con las tensiones circunferenciales:
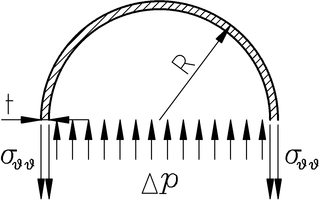
Tensión circunferencial en la botella. Esta tensión es mucho
mayor que la tensión radial (que es como el salto de presión).
Asumimos que la botella es aproximadamente cilíndrica circular.
Esto es al menos cierto hasta llegar al estrechamiento del cuello.
El radio de la botella es R
y el espesor es t.
De esta manera, la tensión circunferencial σθθ
ha de equilibrar en dos veces el espesor (2 t)
el salto de presión Δp en
todo el diámetro (2 R):
σθθ ⋅ 2 t
= Δp ⋅ 2 R,
es decir,
σθθ
= Δp ⋅ (R ⁄ t).
Como la relación R ⁄ t
es grande, la tensión circunferencial σθθ
es mucho mayor que el mero salto de presión Δp. En la bodega de
avión, el salto de presión puede ser perfectamente Δp = 25 kPa; una botella de PET
con un diámetro 2 R = 6 cm
y una pared delgadita de espesor t =
0,25 mm tendría que suportar tensiones circunferenciales
σθθ =
3 MPa, pero el PET puede aguantar cómodamente varias
decenas de megapascales, así que la botella está segura.
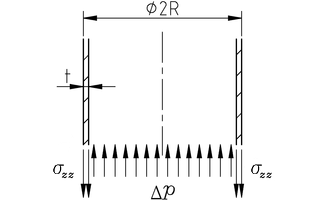
Tensión axial en la botella.
Las tensiones axiales σzz
salen de un cálculo similar al de las tensiones circunferenciales.
La tensión axial repartida en la circunferencia y en el espesor, σzz ⋅ 2 π R t
compensa la presión en la base Δp ⋅ π R2.
La tensión axial es, por lo tanto,
σzz
= Δp ⋅ R ⁄ (2 t).
Esto es la mitad de lo que salió para la tensión circunferencial.

Tensiones debidas a la flexión en la base de la botella. En el
límite elástico, cuando el espesor está completamente agotado,
tomamos como modelo que la mitad del espesor trabaja a compresión
y la otra mitad trabaja a tracción, en ambas mitades con tensión
igual en valor absoluto al límite elástico. Con cargas mayores,
el material se deforma plásticamente en gran magnitud y con poco
esfuerzo y colapsa tras aumentar poco la carga.
Todavía quedan tensiones importantes. La base es más o menos una placa que opera a flexión. Trabajar a flexión significa compensar momentos con tensiones dentro del plano de la placa; en la figura anterior, un momento que obliga a flectar hacia abajo provoca tracción en la parte superior del espesor y compresión en la parte inferior. La teoría elemental de placas (que queda fuera del alcance de este artículo) indica como buena estimación del momento flector por unidad de longitud más grande (que aparece donde la base se encuentra con el lateral) es Δp R2 ⁄ 8. Si asumimos que el material aguanta hasta que se aguanta todo el espesor, de modo que la mitad del espesor está en tracción a la máxima tensión admisible (el límite elástico) y la otra mitad está en compresión también a la máxima tensión admisible, equilibrar el momento flector obliga a que esta tensión sea Δp R2 ⁄ (2 t2). El espesor de 0,25 mm daría una tensión muy falsa, 180 MPa; el PET aguanta unos 55 MPa (quizá más) antes de plastificar, así que necesitamos un espesor como de medio milímetro o más grande en la base y la zona de la pared lateral próxima a la base.
Otros artículos de la serie
- Introducción.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/17/la-botella-y-la-bodega-de-avion-2/
