Deformaciones mecánicas (5)
2017-09-16
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
Los tensores de gradiente de deformación y desplazamiento como formas lineales para el cálculo de diferenciales
Hagamos una descripción lagrangiana de un cuerpo tras experimentar un movimiento. Los puntos materiales, caracterizados por sus posiciones iniciales x, se desplazan de acuerdo con el campo vectorial de desplazamientos u(x) hasta alcanzar las posiciones finales x':
x'(x) ≡ x + u(x).
Introdujimos recientemente los tensores de gradiente de desplazamiento ∇u y de gradiente de deformación ∇x'. Hagamos uso de ellos.
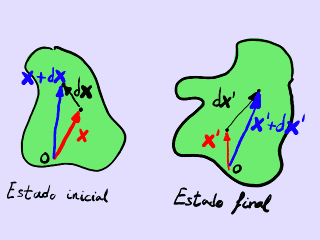
Deformación de un segmento infinitesimal.
Elijamos un segmento infinitesimal du en la configuración inicial del cuerpo. Tras el movimiento, el segmento se convierte en
dx' = ∇x' ⋅ dx = dx + ∇u ⋅ dx = dx + du.
En componentes en ejes cartesianos, la expresión es la siguiente:
dx'i = ∑j(∂x'i ⁄ ∂xj) dxj = dxi + ∑j(∂ui ⁄ ∂xj) dxj = dxi + dui.
El primer sumando es el segmento infinitesimal inicial. El segundo sumando, más interesante, es lo que varía el desplazamiento entre ambos extremos del segmento infinitesimal. El gradiente de deformación proporciona una forma lineal que pasa de segmentos infinitesimales antes del movimiento a segmentos infinitesimales después del movimiento. El gradiente de desplazamientos proporciona una forma lineal que pasa de segmentos infinitesimales antes del movimiento a variaciones infinitesimales en los desplazamientos. Todo esto, por supuesto, es válido cuando el campo de desplazamientos (o la aplicación de posición inicial a posición final) es diferenciable.
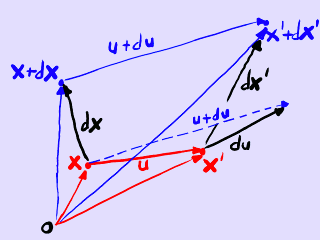
Concepto de variación infinitesimal del desplazamiento.
Categorías: Física
Permalink: https://sgcg.es/articulos/2017/09/16/deformaciones-mecanicas-5/
