Tensiones o esfuerzos mecánicos (17)
2016-06-25
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Hasta ahora, habíamos descrito conceptos aplicables a estados tensionales generales. Hoy vamos a introducir un tipo de estado de tensión muy importante en la práctica: el estado de tensión plana.
Tensión plana
Como ya vimos, las tensiones en el seno de un medio físico están caracterizadas por un tensor de segundo orden. Este tensor es simétrico, así que en el espacio tridimensional queda descrito mediante 6 componentes independientes. La cantidad de información es lo bastante elevada como para que sea conveniente emplear diferentes técnicas gráficas para representar y calcular las propiedades de las tensiones, tales como el elipsoide de Lamé, los círculos de Mohr, la cuádrica indicatriz de tensiones y la cuádrica directriz de tensiones. En algunas situaciones, no obstante, es posible simplificar el tratamiento. Tal es el caso de la tensión plana: cuando las componentes {σxx, σxy, …} del tensor tensión están contenidas en un plano. Si dicho plano es el indicado por los ejes x,y, tal que el eje z es perpendicular al plano, entonces en un estado de tensión plana se cumple la siguiente condición:
σxz = σyz = σzz = 0.
Las demás componentes pueden ser, en general, no nulas.
Otra forma de definir el estado de tensión plana es la siguiente: el vector tensión medido en la dirección perpendicular al plano es nulo. Recordemos el vector tensión t medido en una dirección n cuando el tensor tensión es σ se calcula de la siguiente manera:
t = n ⋅ σ.
En componentes y cuando la dirección de medida es
nx = ny = 0, nz = 1,
el vector tensión queda así:
0 = tx = 0 ⋅ σxx + 0 ⋅ σxy + 1 ⋅ σxz;
0 = ty = 0 ⋅ σxy + 0 ⋅ σyy + 1 ⋅ σyz;
0 = tz = 0 ⋅ σxz + 0 ⋅ σyz + 1 ⋅ σzz.
Estas ecuaciones permiten pasar de una definición de tensión plana a la otra.
El vector tensión siempre está contenido en el plano de tensión plana
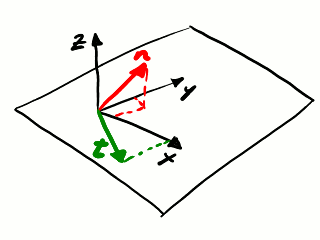
Tensión plana. Para cualquier dirección normal de medida, el
vector tensión está contenido en el mismo plano.
Para una dirección de medida genérica, el vector tensión tiene las componentes siguientes:
tx = nx ⋅ σxx + ny ⋅ σxy + nz ⋅ 0;
ty = nx ⋅ σxy + ny ⋅ σyy + nz ⋅ 0;
tz = nx ⋅ 0 + ny ⋅ 0 + nz ⋅ 0 = 0.
Es decir, el vector tensión siempre está contenido en el plano de tensión plana.
Tensión plana y tensiones principales
Un hecho importante del estado de tensión plana es que una de las tensiones principales es nula y la dirección principal correspondiente es la perpendicular al plano en el que están contenidas las tensiones. La demostración es trivial: el vector tensión medido en la dirección perpendicular al plano de tensión plana es nulo, así que es un múltiplo (nulo en este caso) de la dirección de medida, que es precisamente el requisito que cumplen las tensiones principales. Por ortogonalidad, las otras dos tensiones principales están contenidas en el plano de tensión plana.
Restricciones adicionales
La definción (o las definiciones) que hemos visto de la tensión plana no dicen nada sobre cómo varía el tensor de tensiones. En concreto, nada impide que el tensor de tensiones cambie al tomar medidas en posiciones diferentes según la dirección perpendicular al plano de tensión plana. A menudo, cuando se habla de tensión plana, se hace una restricción adicional que consiste en que el tensor de tensiones no varía según la dirección perpendicular al plano de tensión plana. Este tipo de estado es especialmente fácil de analizar.
Tensión plana en el mundo real
Son muy abundantes las situaciones que se dejan modelar como estados de tensión plana. Por ejemplo, los cuerpos sólidos delgados suelen presentar tensiones que quedan muy bien aproximadas como un estado de tensión plana. Aunque las tensiones en la dirección perpendicular al plano de tensión plana son en general no nulas, suelen ser tan pequeñas que es perfectamente aceptable de cara al análisis fingir que no existen.
Categorías: Física
Permalink: https://sgcg.es/articulos/2016/06/25/tensiones-o-esfuerzos-mecanicos-17/
